Difference between revisions of "Gérard Thibault d'Anvers"

Gérard Thibault d'Anvers
Gérard Thibault d'Anvers
Born	1574
Died	1629
Occupation	Fencing master
Nationality	Dutch
Movement	La Verdadera Destreza
Influences	Jerónimo Sánchez de Carranza ; Luis Pacheco de Narváez ;
Genres	Fencing manual
Language	French
Notable work(s)	Academie de l'Espée (1630)

Latest revision as of 17:07, 31 October 2024

Gérard Thibault d'Anvers (ca. 1574–1629)^[1] was a 17th century Dutch fencing master and author of the 1628 rapier manual Academie de l'Espée, one of the most detailed and elaborate sources ever written on fencing. Details about Thibault's life are sparse and what we know is based on his book and his album amicorum.^[2] The latter contains handwritten notes and celebratory poems from Thibault's friends, relatives, pupils, and colleagues, included among whom are several contemporary fencing masters.^[3]

Thibault was born in or around 1574 in Antwerp, son of Hendrick Thibaut and Margaretha van Nispen.^[4] Although his father used the surname "Thibaut," Gérard used the French form "Thibault."^[4] Hendrick Thibaut came from a well-known family in Ypres, living in Ghent and Antwerp before going into exile in the northern Netherlands.^[4] Henrick's eldest son, Christiaen, founded the noble family Thibaut van Aegtekerke.^[5]

Thibault first studied fencing in Antwerp under Lambert van Someron, who taught between the years of 1564 and 1584.^[6] In 1605, Thibault was a wool merchant in Sanlúcar de Barrameda, south of Seville on the Guadalquivir river, and the hometown of Jerónimo Sánchez de Carranza.^[2] There, he took an interest in fencing, studying the Spanish rapier system of Destreza.^[2]

Thibault left Spain to return to the Netherlands, and was in Amsterdam as early as 1610.^[2] In or around 1611, he presented his system to an assembly of Dutch masters at a competition in Rotterdam.^[7] Thibault won first prize, earning an invitation to the court of Prince Maurice of Nassau, where the Prince observed Thibault's system in a multi-day demonstration.^[6]

Although initially met with skepticism, Thibault convinced his fellow Dutch fencing masters, including Johannes Damius of Haarlem, Dirck van Stervergen of Leiden, Cornelis Cornelisz van Heusden of Amsterdam, and Thibault's former teacher Lambert von Someron.^[6] In 1615, Thibault was invited to the court at Cleves and left Amsterdam, where he once again demonstrated his system successfully.^[8] Over the next several years, Thibault traveled from Cleves, Amsterdam, to Spain, back to Amsterdam, and finally to Leiden in 1622.^[9] There, Thibault studied mathematics at Leiden University.^[10] It is unclear whether Thibault taught his system at the university.^[10] It is during his time in Leiden that Thibault likely began working on Academie de l'Espée and employed a team of sixteen master engravers.^[11]

Thibault died in 1629, a year before his masterpiece was finally published (despite the date on the title page of 1628, it was not published until 1630).^[12]

Treatise

The Academie de l'Espée (1630) is presented in two books. Book 1 consists of a short introduction, populated with plates showing the coats of arms of several nobles who were prominent in and around the court of the low countries at the time he wrote this book, and then introduces training in the use of his system of swordplay.

Thibault, although he does not explain until Plate 8, uses the term estocade to describe a thrust to the near, right side, and the term imbrocade to describe a thrust to the far, left side, from the Italian terms stoccata and imbroccata. English has a single term thrust to mean either, but did borrow the Italian term imbroccata to specifically refer to the latter type of thrust.

Plate I begins with a long philosophical discussion of his worldview. It is a good insight into the late Renaissance worldview relating mathematics and Christian religious beliefs to an idealized human figure. It then explains how to construct his Mysterious Circle. This includes a lengthy discussion of how the circle relates geometrically to the ideal body size, based on Vitruvius, and notes about how the lines and crossing points of the circle will be used. This is the basic reference diagram for the entire system. It also includes explanations of how to measure for the correct sword size for any given person, and some explanation of why this is so, and some introductory explanation of appropriate ranges for swordplay.

Plate II compares his ideal body measurements against a figure by Albrecht Durer. Part 2 discusses his ideal sword scabbard and how to construct and wear it.

Plates III & IV deal with how to properly draw a sword and how to approach an adversary.

Plate V introduces his fighting system. First, how to deal with feints (typical of the schools of the time) and defend against typical thrusts.

Plate VI introduces several basic concepts. The importance of maintaining contact between swords, not typical of schools of the time, and the basic steps to close with and thrust into an opponent. The first steps show the attack as if he were to make no defense. Then he assumes the opponent will try to disrupt the attack, and discusses how to deal with interruptions if they occur at various points during the movement.

Plate VII introduces an opponent using circular disengagements and counterthrusts to disrupt an attack, and how to counter them.

Plate VIII introduces the imbroccata attack against the left side and exercises to counter them when they occur at various stages of the attack.

Plates IX & X introduces the idea of blade control and resistance using various degrees of force which can be applied against the blade to parry an attack. He defines several increasing degrees of pressure and introduces exercises to learn to distinguish them, and how to counter parries by force. His recommendation to pursue a course of study, rather than master all the lessons from Plate IX to XIII before begining to practice the exercise in Plate XV, where he introduces attacking to the right hand side, but for practical training, to pair up the lessons of attacks to the outside line with those to the inside line. That is, do the exercises from Plate IX then Plate XV, Plate X with Plate XVI, and so on, practising each in turn. This way, the student learns to fight to both left and right hand side while acquiring increasing skills and ability.

Plate XI continues the exploration of how to deal with different degrees of force against the blade.

Plate XII shows how to create an angle between blades to move in against the opponent

Book 2 lacks an explanation of the complex frontspiece, and was incomplete at the time of his death, but what he does have shows how to use his style against other systems and weapons then in use, including shields, longsword, and firearms.

The plates uploaded to WikTenauer are sufficient to follow the text, but if anyone wishes to see very high definition images, they can be found on www.geheugenvannederland.nl. Search on Girard Thibault.

Illustrations	Translation by Bruce G. Hearns	Transcription by Bruce G. Hearns
	Academy of the Sword by Girard Thibeault of Antwerp, wherein is demonstrated by means of mathematical rules, upon the foundation of the mysterious Circle, the Theory and Practise of the true and, until present, unknown secrets of the handling of arms both on foot and on horseback. M.DC.XXXVIII (1628)	Academie de L'ESPÉE de Girard Thibault d'Anvers ou ſe demonſtrent par Reigles mathematiques ſur le fondemont d'un Cercle mysterieux la theorie et pratique des vrais et iuſq'a preſent incognus ſecrets du maniement DES ARMES a Pied et a Cheval. M.DC.XXVIII
	In tranquil reason, not impatient in his work, leads us courageously along his meandering path. Gerard Thibault of Antwerp Rejoice. Patience endures.	TRANQVILLA RATIO, NEC SVI IMPATIENS LABOR, MODUM EVAGANTI PRÆSTRVIT FEROCIÆ. Gerard Tibault d'Anvers Gaudet Patientia duris
	To the valliant heart, nothing is impossible. Arms and sundry titles of George William (1595 – 1640) of the House of Hohenzollern, Elector of Brandenburg and Duke of Prussia from 1619.	Au coeur vaillant rien n'est impossible Serenissimo Principi ac Domino Domino Georgio Guilermo Marchioni Brandenburgensi S. Romani imperii Archicamerario et Electori; Borussiæ, Iuliæ, Cliviæ, Montium Stetini, Pomeraniæ, Cassubiorum, Vandalorum et in Silesia Crosnæ, Carnovi, æ’que Duci Burggravio Norimbergensi Principi Rugiæ. Comiti Marchiæ, ac Ravensbergi. Dynatæ Ravenstein y, &c.
	Work well without pause, and the hours pass quickly. Arms and sundry titles of Johan Sigismund (1572 – 1619), Elector of Brandenburg (1608 – 1619) of the House of Hohenzollern, Elector of Brandenburg from 1608 and Duke of Prussia, through his wife Anna, from 1618.	Fais biens sans demeure, et peu de temps se passe l’heure Serenissimo Principi ac Domino Do. Io. Achimo Sigismundo. Marchioni Brandenburgensi, Borussiæ, Iuliæ, Cliviæ, Montium Stetini, Pomeraniæ, Cassubiorum, Vandalorum, et in Silesia Crosnæ, Carnoviæ ‘que Ducter
	Everything with God, Nothing without Reason. Arms and title of Christian (the Elder) (1566 - 1633), Duke of Brunswick and Lunenbourg.	Tout Avec Dieu, Rien Sans Raison Serenissimo Principi ac Domino Domino Christiano Duci Brunswicensi et Lunenburgensi
	(Order of the Garter about the arms – Shame to him who evil thinks) I maintain Arms and titles of Maurice of Nassau (1567 - 1625), who became Prince of Orange in 1618.	(Order of the Garter about the arms – Honi soit qui mal y pense) Ie Maintiendray Ilustrissimo Heroi Muritio Principia Auraico, Comiti Nassoviæ, Cattimeliboci, Viandæ, Diestii, Lingæ, Mursiæ, Bueræ, Leerdami, &c. Marchioni Veriæ, ac Frissinge Baroni Bredæ. Civitatis Graviæ, ac ditionis Cuyckiæ, Herrstas, Cranendonc, Warneston, Arlaii, Svti Viti. Daesburgi &c. Vicecomiti Hæreditario Antwerpiæ, et Bizantii &c. Gubernatoi Geldriæ, Hollandie,, Lelandiæ, Westfrisiæ Zutphaniæ, Ultraiecti, Transisalaniæ, Groninge et Omlandiæ; Summo earundem Provinciarum terra mario, misitiæ Duci
	Of the homeland. With the homeland. Arms and titles of Frederick Henry (1584 - 1647), Prince of Orange (1625-1647)	Patriæ. Patrique Illustrissimo Principi ac Domino D. Frederico Henrico Principi Auraico. Comiti Nassoviæ, Dominio Geertrudis-bergæ, utriusque Swaluæ, Naeldwici. Marischalco Hæreditario Hollandiæ, Unitarum Provinciarum Equitum Præfecto Generali &c.
	Constant Arms & titles of Ernest Casimir (1573-1632), Count of Nassau-Dietz (1606-1632)	Constant Illust[rissi]mo Principi Ernesto Casimiro Comiti Nassoviæ, Catimeliboci, Viandæ, Dies Rii; Domino Bilsteiniæ, Castrorum Unitarum Provenciarum Praefecto; Gubernatori Frisiæ &c.
	God and all Dedication and Arms of Simon VII (1587-1627), Count of Lippe (1613-1627), and his brother Otto (1589 – 1657), Count of Lippe-Brake (1621-1657)	Deo et Cunctis Generosis vere’q Germanis Fratribus, Simoni et Otthoni, Comitibus et Nobisibus Dominis de Lippia
	Nothing without God Arms of Stephan Gans, Baron Putlitz	Rien sans Dieu Nobilissimo, Generosissimoq; Heroi Domino Stephano Gans, Libero Baroni PotlitzI, Nec non Wolffshagiæ, turmæ equestris sub ductu et moderamine Illustrissimi Principis Auraici præfecto
	Arms of Louis XIII Louis de Bourbon, called the Just, by grace of God, most-Christian King of France and Navarre, thirteenth of this name. 1628	LOVIS DE BOVRBON DICT LE IUSTE PAR LA GRACE DE DIEV TRES-CHESTIEN ROY DE FRANCE ET DE NAVARRE. TREIZIESME DE CE NOM 1628
	To the most august, most high, most powerful, high, magnficent Emperors, Kings, Princes, Dukes, Counts, and all other Lords and noble Teachers and Amateurs, of the most noble science of handling Arms	Aux tresauguste, treshaults, trespuissants, tresillustres, hautes, magnfiques, Empereur Roys Princes Ducs Comtes et touts autres seigneurs et nobles Fauteurs & Amateurs de La tresnoble science de manier les armes
		In nob. Et eximii viri D. GERARDI THIBAULTII Gladiatoriam artem, symbolo ac praemio ab illustrissimo principe Mavritio à Nassau, &c. Donatam. Inter ſe geminas ferro concurrere dextras, Fortuna ſuerat, nunc erit artis opus. Nam hoc Roma parens, quamuis Mauortia, non hoc Lećtorem docuit Gratia tota ſuum. Temporibus noſstris, ipſa ſe teſte, vetuſtas Vincitur, & faſſas dat ſupera manus; Artis inops: totus quam dum confiderat orbis, Tyronem unius ſe videt eſſe viri. Hanc rude donatus Veianius ineret arenam. Intrata eſt numquam dicet arena mibi. Trecius au debit cum Myrmillone ſub armis Stare, nec hic illi jam metuendus erit. Hanc Samnis teneat, teneat qui prouocat, artem; Ignauo neuter ſanguine tinget hamum. Hanc colit, hac noſstrum Thibautius imbuit auum, Hanc nondum genitis nobile donat opus. Nec negat hoc Martis ſoboles Naſſovius Heros, Et jam victori præmia certa dedit: Inſtrućtorque operis, plauſuque opibusque parenti Adfuit, & partem vindicat ipſe ſibi. Quælibet arguto peragenda eſt judice cauſa: Hac à non victo Pricipe palma datur. D. Heinsius
	GRANT OF PRIVILEGE BY THE KING OF FRANCE By grace and privilege of the King, it has been permitted and granted to Gerard Thibault native of Antwerp, to print, sell, and distribute the present book and figures, in such character and volume as to him seems fit, in all the Kingdoms, lands, and holdings of his Majesty during a period of nine years counting from the day he shall have it printed, with all protections from all persons of whatever quality and condition they may be, to sell and distribute the said book, in part or portion thereof, whether a lithograph, woodcut, etched plate, stolen or counterfeit, or to sell the said figures alone or with summary of what they represent, either separately or jointly, on pain of contravention of loss of goods and five thousand pounds fine, half applicable to his Majesty, and the other to the said Thibault; who, moreover carries full letters to this effect, given in Paris, the XXI Day of December, in the year of grace one thousand six hundred and twenty and in fourth of the reign of the said King. Signed by the King in his Council and sealed with the great seal of his Majesty in yellow wax on a ribbon.	EXTRAICT DU PRIVILEGE DU ROY DE FRANCE Par grace & privilege du Roy, il a eſté permis & oćtroyé à Gerard Thibault natif d'Anvers, d'imprimer vendre & debiter le preſent livre & figures, en tel charaćter & volume que bon luy ſemblera, par tous les Royaumes pays terres & Seigneuries de ſa Majeſté, pandant le temps de neuf ans à compter du jour qu'il ſera achevé d'imprimer: avec deffences à toutes perſonnes de quelque qualité & condition qu'ils ſoyent, de vendre & debiter ledićt livre part ou portion d'iceluy, avec leſdites figures ſeuls ou ſans icelles, ſoit taille douce, de bois, d’eau forte, de le pocher ou contrefaire, ou vendres leſdites figures ſeules ou avec ſomaire de ce qu'elles repreſentent, ſoit ſeparemant ou conjoinćtment, ſur pene au contrevenant de perte des exemplaires, & de cincq mille livres d'amande; moitie applicable à ſa Majeſté, & l'autre audićt Thibault; comme plus a plein eſt porté aux lettres ſur ce obtenues, données à Paris le XXI. Jour de Decembre, l'an de grace mil ſix cent vengt, & du regne du dićt Seigneur le quatieſme. Seignées par le Roy en ſon Conſeil Perrochet, & ſcellees du grand ſeau de ſa Maieſté en cire jaune à queue pendant.
	PRIVILEGE The Estates General of the United Provinces of the Netherlands, have consented and granted, and do consent and grant to the named Gerald Thibault, that be during the time of next thirty years to come, alone in these united Lands, affiliated lands and towns, full rights and privileges that he may print, sell, and distribute this treatise, engravings, instructions, knowlege, & exercises entitled “Academie de GIRARD THIBAULT d'Anvers, ou ſe demonſtrent d'un cercle mysſterieus la theorie & praćticque des vrais, & juſtes à preſent ingcognus ſecrets du maniement de Armes à pied & à cheval.” Forbidding one and all within the jursdiction of these lands, to offer for sale copies of the aforesaid book for the aforsaid time of thirty years, directly or indirectly, in whole, or in part either greater or lesser, neither the imprint, nor the engravings, nor the explanations of the engravings. Upon pain of forfeture of all copies and payment of a fine of the sum of nine hundred guilders. One third part thereof to be given to the officer who performed the arrest, the second third to the watchmen, and the remaining third to the aforesaid Girardo Thibault. Given in Graven-Hague this fifth of June Sixteen-Twenty-Seven. Gaspar van Vosgbergen. By order of the President of the Estates-General. I. van GOCH.	PRIVILEGIE De Staten Generael der Vereenighde Nederlanden, hebben gheconſenteert ende gheoćtroyeert, conſenteren ende oćtoyeren by deſen d'erfghanamen van Giraldo Thibault, dat ſy gheduerende den tijdt van dertich eerſt-ckomende Iaren, alleene in deſe vereenighde Landen, gheaſſocieerde Landtſchappen ende Steden, ſullen moghen Drucken, doen Drucken, ende uytgheven ſeeckere Wapen-kunſt, beſtaende in Figuren, met regulen, aenwijſinghen ende leer-ſstucken, gheinſituleert Academie de GIRARD THIBAULT d'Anvers, ou ſe demonſtrent d'un cercle mysſterieus la theorie & praćticque des vrais, & juſtes à preſent ingcognus ſecrets du maniement de Armes à pied & à cheval. Verbiedende allen ende een yeghelijck Ingheſetenen van deſe Landen, de voorſchreven Wapen-konſte binnen den voorſchreven tijdt van dertich Iaren, direćtelijck ofte indirećtelijck, in't geheel, ofte ten deele, in't groot oſte in't kleyne, na te Drucken, ende uyt te gheven, oſte elders na ghedruct, hier te Lande te brenghen om verkoſt te werden, by verbeurte van alle de na-ghedruckte exemplaren, ende daer-en-boven van de ſomme van neghen hondert guldens; 'tappliceren een derdendeel daer van ten behoeve van Officier die de calangie doen ſal, het tweede derdendeel ten behoeve van de armen, ende het reſterend derdendeel ten behove van de voorſchreven erfghenamen van Girardo Thibault. Ghedaen in s'Graven-Haghe op den vijfden Iunij ſeſthein-hondert ſeven en twintich. Gaſpar van Vosberghen Vt. Ter ordonnantie van de Hooch-ghemelte Heeren Staten Generael. I. van GOCH
	NOTICE CONCERNING the figures of this book.	AVERTISSEMENT SVR LA CONSI- deration des figures de ce livre.
	Because the reader shall find it strange that many of the images are not placed upon the ground, but are above or below the horizon, we think it best they be conceived of as paintings upon the walls; this being because of the unequal circles above the horizon compared to the ground, and for more convenient representation of the doctrine, & for easier intelligbility in a manner which does not extend perspectives. Thus in Plate 3, high on both sides, we see 4 men painted on the walls, & in Plate 5 there are four pieces in the form of paintings in the middle of the masonry wall each with its own appropriately-sized circle. In Plates 6, 16, 21, 22, 25, & 28 we find painted canvasses & murals on the sides, and on the lower parts of the walls. In Plates 7 & 27 we understand they are made in the form of charts. In Plate 19, a tapestry hangs in the middle, in which the doctrines are embroidered. The Plates 5, 8, 14, 17, 18, 20, 22, 25, 26, 27, 28, & 29 likewise have painted walls, but the most important parts are shown alive on the ground or as painting on the wall base, because we have put there the means to see how the position of the swords relates to the lines of the Circle in the form of shadows on the lower line or base. We can see the positions of the blades, on the ground of the circle, by which means the capability to work out the movements of the swords the figures have in their hands becomes quite easy.	Pource que le ſpećtateur trouveroit eſtrange, que pluſieurs Images ne ſont fixement poſées ſur le fondement, taut au deſſus qu'au deſſoubs de l'Horiſon: nous avons touvé bon de l'advertir, qu'il les faut concevoir comme eſtant deſpeintes aux murailles; cela eſtant fait à cauſe des Cercles inegaux tant au deſſus de l'Horiſon que ſur le plan, pour la repreſentation plus commode de la doćtrine, & pour l'intelligence plus facile du commun qui n'entend les perſpećtives: ainſi au Tableau 3. au deſſus d'un & d'autre coſté ſont deſpeints 4. hommes aux parois, & en la Table 5. il y à quatre pieces en forme de peinture au millieu de la muraille ou maſſonerie, deſquels Cercles chaſcun ſuſſit pour ſoy, & es Tables 6. 16. 21. 22. 25. & 28. au millieu des toilles peinturées, & au coſtez ſont deſpeintes à la paroy, es Tables 7. & 27. faut entendre que cela eſt fait en forme de chartes, & en la Table 19. un tapi tendu ou pendu au millieu, dans leſquel les doćtrines ſont tiſſues, & es Tables 5. 8. 14. 17. 18. 20. 22. 25. 26. 27. 28. 29. de meſme deſpeint aux murailles, mais les premieres pieces ſe demonſtrent plus vivement ſur le fond ou baſe que les autres, car la ſe voit la façon des accords des eſpées & leur operation par les lignes du Cercle; pour ce que en forme d'Eſquierre de la ligne Inferieure ou baſe, on trouve un accord des lames, fait au fond ou Cercle, par lequel le jugement des operations mouvantes des eſpées que les figures tiennent en main, eſt rendu tres-facile.

Main article: Gérard Thibault d'Anvers/Plates 1-11

Main article: Gérard Thibault d'Anvers/Plates 12-22

Main article: Gérard Thibault d'Anvers/Plates 23-33

For further information, including transcription and translation notes, see the discussion page.

Work	Author(s)	Source
Images	courtesy of Reinier van Noort	Thibault.zip
Translation	Bruce G. Hearns	Wiktenauer
Transcription	Bruce G. Hearns	Wiktenauer

Additional Resources

Howden, Matthew. "Comparison of Thibault’s Circle and the Leiden Circle". Sworded Contemplations. April, 2008. Retrieved 08 February 2015.

The following is a list of publications containing scans, transcriptions, and translations relevant to this article, as well as published peer-reviewed research.

Fontaine Verwey, Herman de la (1978). "Gerard Thibault and his Academie de l'Espée." Quaerendo 8(4): 283-319. doi:10.1163/157006978X00188.
Majár, János; Zoltán Várhelyi (2014). "Thibault and Science I. Measure, Distances and Proportions in the Circle." Acta Periodica Duellatorum 2(1): 67-104. doi:10.1515/apd-2015-0014.
Johann Georg Pascha; Heinrich von und zum Velde (2018). Proper Description of Thrust-Fencing with the Single Rapier. Trans. by Reinier van Noort; Jan Schäfer. Glasgow: Fallen Rook Publishing. ISBN 978-0-9934216-7-9.
Thibault, Gérard (2006). Academy of the Sword. Trans. by John Michael Greer. Highland Village, TX: Chivalry Bookshelf. ISBN 978-1891448409.
Thibault, Gérard (2017). Academy of the Sword. Trans. by John Michael Greer. London: Aeon Books. ISBN 978-1-190465-884-9.
Van Noort, Reinier; Jan Schäfer (2017). "An analysis and comparison of two German thrust-fencing manuscripts." Acta Periodica Duellatorum 5(1): 63-74. doi:10.36950/apd-2017-002.

References

↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.288, 297
↑ ^2.0 ^2.1 ^2.2 ^2.3 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.289
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.297
↑ ^4.0 ^4.1 ^4.2 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288-289
↑ ^6.0 ^6.1 ^6.2 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.290
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.289-290
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.294
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.294-296
↑ ^10.0 ^10.1 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.296
↑ de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.296, 310
↑ Thibault, Gérard. Academy of the Sword. Trans. John Michael Greer. Highland Park, TX: The Chivalry Bookshelf, 2006. pp 1-2.

[1] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.288, 297

[Verwey.2C_Herman_Fontaine_1978_p.289-2] 2.0 ^2.1 ^2.2 ^2.3 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.289

[3] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.297

[Verwey.2C_Herman_Fontaine_1978_p.288-4] 4.0 ^4.1 ^4.2 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288

[5] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288-289

[Verwey.2C_Herman_Fontaine_1978_p.290-6] 6.0 ^6.1 ^6.2 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.290

[7] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.289-290

[8] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.294

[9] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.294-296

[Verwey.2C_Herman_Fontaine_1978_p.296-10] 10.0 ^10.1 de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.296

[11] Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.296, 310

[12] Thibault, Gérard. Academy of the Sword. Trans. John Michael Greer. Highland Park, TX: The Chivalry Bookshelf, 2006. pp 1-2.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Difference between revisions of "Gérard Thibault d'Anvers"

Latest revision as of 17:07, 31 October 2024

Contents

Treatise

Book 1 - Introduction. Arms of Patrons and supporters of Thibault

Book 1 - Tableau / Plates I - XI

Book 1 - Tableau / Plates XII - XXII

Book 1 - Tableaux / Plates XII - XXII

Copyright and License Summary

Additional Resources

References

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Navigation:

Jump to:

Community:

Tools

donate

@@ Line 45: / Line 45: @@
 Thibault was born in or around 1574 in Antwerp, son of Hendrick Thibaut and Margaretha van Nispen.<ref name="Verwey, Herman Fontaine 1978 p.288">de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288</ref> Although his father used the surname "Thibaut," Gérard used the French form "Thibault."<ref name="Verwey, Herman Fontaine 1978 p.288"/> Hendrick Thibaut came from a well-known family in Ypres, living in Ghent and Antwerp before going into exile in the northern Netherlands.<ref name="Verwey, Herman Fontaine 1978 p.288"/> Henrick's eldest son, Christiaen, founded the noble family Thibaut van Aegtekerke.<ref>de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.288-289</ref>
-Thibault first studied swordsmanship in Antwerp under Lambert van Someron, who taught between the years of 1564 and 1584.<ref name="Verwey, Herman Fontaine 1978 p.290">de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.290</ref> In 1605, Thibault was a wool merchant in Sanlúcar de Barrameda, south of Seville on the Guadalquivir river, and the hometown of Jerónimo Sánchez de Carranza.<ref name="Verwey, Herman Fontaine 1978 p.289">de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.289</ref> There, he took an interest in swordsmanship, studying the Spanish rapier system of Destreza.<ref name="Verwey, Herman Fontaine 1978 p.289"/>
+Thibault first studied fencing in Antwerp under Lambert van Someron, who taught between the years of 1564 and 1584.<ref name="Verwey, Herman Fontaine 1978 p.290">de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.290</ref> In 1605, Thibault was a wool merchant in Sanlúcar de Barrameda, south of Seville on the Guadalquivir river, and the hometown of Jerónimo Sánchez de Carranza.<ref name="Verwey, Herman Fontaine 1978 p.289">de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) p.289</ref> There, he took an interest in fencing, studying the Spanish rapier system of Destreza.<ref name="Verwey, Herman Fontaine 1978 p.289"/>
 Thibault left Spain to return to the Netherlands, and was in Amsterdam as early as 1610.<ref name="Verwey, Herman Fontaine 1978 p.289"/> In or around 1611, he presented his system to an assembly of Dutch masters at a competition in Rotterdam.<ref>de la Verwey, Herman Fontaine. "Gerard Thibault and his Academie de l'Espée," Quaerendo VIII (1978) pp.289-290</ref> Thibault won first prize, earning an invitation to the court of Prince Maurice of Nassau, where the Prince observed Thibault's system in a multi-day demonstration.<ref name="Verwey, Herman Fontaine 1978 p.290"/>
@@ Line 56: / Line 56: @@
 == Treatise ==
-The ''[[Academie de l'Espée (Gérard Thibault d'Anvers)|Academie de l'Espée]]'' (1630) is presented in three parts, a short introduction, populated with plates showing the coats of arms of several nobles who were prominent in and around the court of the low countries at the time he wrote this book, Book 1, which deals with training in the use of his system of swordplay, and Book 2 which shows how to use his system against other systems and weapons, including shields, longsword, and firearms.
+The ''[[Academie de l'Espée (Gérard Thibault d'Anvers)|Academie de l'Espée]]'' (1630) is presented in two books. Book 1 consists of a short introduction, populated with plates showing the coats of arms of several nobles who were prominent in and around the court of the low countries at the time he wrote this book, and then introduces training in the use of his system of swordplay.
+Thibault, although he does not explain until Plate 8, uses the term ''estocade'' to describe a thrust to the near, right side, and the term ''imbrocade'' to describe a thrust to the far, left side, from the Italian terms ''stoccata'' and ''imbroccata''. English has a single term ''thrust'' to mean either, but did borrow the Italian term ''imbroccata'' to specifically refer to the latter type of thrust.
+Plate I begins with a long philosophical discussion of his worldview. It is a good insight into the late Renaissance worldview relating mathematics and Christian religious beliefs to an idealized human figure. It then explains how to construct his <i>Mysterious Circle</i>. This includes a lengthy discussion of how the circle relates geometrically to the ideal body size, based on Vitruvius, and notes about how the lines and crossing points of the circle will be used. This is the basic reference diagram for the entire system.
+It also includes explanations of how to measure for the correct sword size for any given person, and some explanation of why this is so, and some introductory explanation of appropriate ranges for swordplay.
+Plate II compares his ideal body measurements against a figure by Albrecht Durer. Part 2 discusses his ideal sword scabbard and how to construct and wear it.
+Plates III & IV deal with how to properly draw a sword and how to approach an adversary.
+Plate V introduces his fighting system. First, how to deal with feints (typical of the schools of the time) and defend against typical thrusts.
+Plate VI introduces several basic concepts. The importance of maintaining contact between swords, not typical of schools of the time, and the basic steps to close with and thrust into an opponent. The first steps show the attack as if he were to make no defense. Then he assumes the opponent will try to disrupt the attack, and discusses how to deal with interruptions if they occur at various points during the movement.
+Plate VII introduces an opponent using circular disengagements and counterthrusts to disrupt an attack, and how to counter them.
+Plate VIII introduces the imbroccata attack against the left side and exercises to counter them when they occur at various stages of the attack.
+Plates IX & X introduces the idea of blade control and resistance using various degrees of force which can be applied against the blade to parry an attack. He defines several increasing degrees of pressure and introduces exercises to learn to distinguish them, and how to counter parries by force. His recommendation to pursue a course of study, rather than master all the lessons from Plate IX to XIII before begining to practice the exercise in Plate XV, where he introduces attacking to the right hand side, but for practical training, to pair up the lessons of attacks to the outside line with those to the inside line. That is, do the exercises from Plate IX then Plate XV, Plate X with Plate XVI, and so on, practising each in turn. This way, the student learns to fight to both left and right hand side while acquiring increasing skills and ability.
+Plate XI continues the exploration of how to deal with different degrees of force against the blade.
+Plate XII shows how to create an angle between blades to move in against the opponent
+Book 2 lacks an explanation of the complex frontspiece, and was incomplete at the time of his death, but what he does have shows how to use his style against other systems and weapons then in use, including shields, longsword, and firearms.
+The plates uploaded to WikTenauer are sufficient to follow the text, but if anyone wishes to see very high definition images, they can be found on [http://www.geheugenvannederland.nl/ www.geheugenvannederland.nl]. Search on Girard Thibault.
 {{master begin
-  | title = Academie de L'ESPÉE - Book 1 - Introduction - Arms of Patrons and supporters of Thibault
+  | title = Book 1 - Introduction. Arms of Patrons and supporters of Thibault
-  | width = 75em
+  | width = 90em
 }}
-{| class="wikitable"
+{| class="master"
-! Images
+! Illustrations
 ! Translation by <br/> [[user:Bruce Hearns|Bruce G. Hearns]]
 ! Transcription by <br/>[[user:Bruce Hearns|Bruce G. Hearns]]
 |- style="font-family: times, serif; vertical-align:top"
 |[[File:Academie de l'Espée Title.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-0| Large Version]]
 |'''''Academy of the Sword''''' by Girard Thibeault of Antwerp, wherein is demonstrated by means of mathematical rules, upon the foundation of the mysterious Circle, the Theory and Practise of the true and, until present, unknown secrets of the handling of arms both on foot and on horseback.
@@ Line 80: / Line 107: @@
 |- style="font-family: times, serif; vertical-align:top"
 |[[File:Thibault L1 Intro 02.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/portret%20girard%20thibault%20delff%20willem%20jacobsz?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-008| Large Version]]
 |In tranquil reason, not impatient in his work, leads us courageously along his meandering path.
@@ Line 97: / Line 122: @@
 |- style="font-family: times, serif; vertical-align:top"
 |[[File:Thibault L1 Intro 03.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20georg%20wilhelm%20keurvorst%20brandenburg?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-002| Large Version]]
 |To the valliant heart, nothing is impossible.
-Arms and sundry titles of [[https://en.wikipedia.org/wiki/George_William,_Elector_of_Brandenburg|George William]] (1595 – 1640), Elector of Brandenburg (1619 – 1640).
+Arms and sundry titles of [https://en.wikipedia.org/wiki/George_William,_Elector_of_Brandenburg George William] (1595 – 1640) of the House of Hohenzollern, Elector of Brandenburg and Duke of Prussia from 1619.
 |Au coeur vaillant rien n'est impossible
@@ Line 111: / Line 134: @@
 |[[File:Thibault L1 Intro 04.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20johann%20sigismund%20keurvorst%20brandenburg?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-003| Large Version]]
 | Work well without pause, and the hours pass quickly.
-Arms and sundry titles of [[https://en.wikipedia.org/wiki/John_Sigismund,_Elector_of_Brandenburg|Johan Sigismund]] (1572 – 1619), Elector of Brandenburg (1608 – 1619)
+Arms and sundry titles of [https://en.wikipedia.org/wiki/John_Sigismund,_Elector_of_Brandenburg Johan Sigismund] (1572 – 1619), Elector of Brandenburg (1608 – 1619) of the House of Hohenzollern, Elector of Brandenburg from 1608 and Duke of Prussia, through his wife Anna, from 1618.
 |Fais biens sans demeure, et peu de temps se passe l’heure
@@ Line 126: / Line 147: @@
 |[[File:Thibault L1 Intro 05.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20christiaan%20hertog%20brunswijk%20nenburg?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-004| Large Version]]
 |Everything with God, Nothing without Reason.
-Arms and title of [[https://en.wikipedia.org/wiki/Christian,_Duke_of_Brunswick-Lüneburg|Christian (the Elder)]] (1566 - 1633), Duke of Brunswick and Lunenbourg.
+Arms and title of [https://en.wikipedia.org/wiki/Christian,_Duke_of_Brunswick-Lüneburg Christian (the Elder)] (1566 - 1633), Duke of Brunswick and Lunenbourg.
 |Tout Avec Dieu, Rien Sans Raison
@@ Line 139: / Line 158: @@
 |[[File:Thibault L1 Intro 06.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20maurits%20prins%20oranje?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-005| Large Version]]
 |(Order of the Garter about the arms – Shame to him who evil thinks)
 I maintain
-Arms and titles of [[https://en.wikipedia.org/wiki/Maurice,_Prince_of_Orange|Maurice]] (1567 - 1625), Prince of Orange (1618 – 1625)
+Arms and titles of [https://en.wikipedia.org/wiki/Maurice,_Prince_of_Orange Maurice] of Nassau (1567 - 1625), who became Prince of Orange in 1618.
 |(Order of the Garter about the arms – Honi soit qui mal y pense)
@@ Line 157: / Line 174: @@
 |[[File:Thibault L1 Intro 07.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20frederik%20hendrik%20prins%20oranje?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-006| Large Version]]
 |Of the homeland. With the homeland.
-Arms and titles of [[https://en.wikipedia.org/wiki/Frederick_Henry,_Prince_of_Orange|Frederick Henry]] (1584 - 1647), Prince of Orange (1625-1647)
+Arms and titles of [https://en.wikipedia.org/wiki/Frederick_Henry,_Prince_of_Orange Frederick Henry] (1584 - 1647), Prince of Orange (1625-1647)
 |Patriæ. Patrique
@@ Line 174: / Line 189: @@
 |Constant
-Arms & titles of [[https://en.wikipedia.org/wiki/Ernest_Casimir_I,_Count_of_Nassau-Dietz|Ernest Casimir]] (1573-1632), Count of Nassau-Dietz (1606-1632)
+Arms & titles of [https://en.wikipedia.org/wiki/Ernest_Casimir_I,_Count_of_Nassau-Dietz Ernest Casimir] (1573-1632), Count of Nassau-Dietz (1606-1632)
 |Constant
@@ Line 186: / Line 201: @@
 |God and all
-Dedication and Arms of [[https://en.wikipedia.org/wiki/Simon_VII,_Count_of_Lippe|Simon VII]] (1587-1627), Count of Lippe (1613-1627), and his brother [[https://en.wikipedia.org/wiki/Otto,_Count_of_Lippe-Brake|Otto]] (1589 – 1657), Count of Lippe-Brake (1621-1657)
+Dedication and Arms of [https://en.wikipedia.org/wiki/Simon_VII,_Count_of_Lippe Simon VII] (1587-1627), Count of Lippe (1613-1627), and his brother [https://en.wikipedia.org/wiki/Otto,_Count_of_Lippe-Brake Otto] (1589 – 1657), Count of Lippe-Brake (1621-1657)
 |Deo et Cunctis
@@ Line 195: / Line 210: @@
 |[[File:Thibault L1 Intro 10.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20stephanus%20baron%20lotsitzi?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-007| Large Version]]
 |Nothing without God
-Arms of Stephan Gans, [[https://en.wikipedia.org/wiki/Gans_zu_Putlitz|Baron  Putlitz]]
+Arms of Stephan Gans, [https://en.wikipedia.org/wiki/Gans_zu_Putlitz Baron  Putlitz]
 |Rien sans Dieu
@@ Line 209: / Line 222: @@
 |[[File:Thibault L1 Intro 11.jpg|200px]]
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/wapen%20lodewijk%20xiii%20koning%20frankrijk?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-001| Large Version]]
 |Arms of Louis XIII
-[[https://en.wikipedia.org/wiki/Louis_XIII_of_France|Louis]] de Bourbon, called the Just, by grace of God, most-Christian King of France and Navarre, thirteenth of this name.
+[https://en.wikipedia.org/wiki/Louis_XIII_of_France Louis] de Bourbon, called the Just, by grace of God, most-Christian King of France and Navarre, thirteenth of this name.
@@ Line 330: / Line 341: @@
 |- style="font-family: times, serif; vertical-align:top"
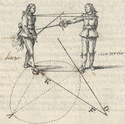
+| class="noline" | Because the reader shall find it strange that many of the images are not placed upon the ground, but are above or below the horizon, we think it best they be conceived of as paintings upon the walls; this being because of the unequal circles above the horizon compared to the ground, and for more convenient representation  of the doctrine, & for easier intelligbility in a manner which does not extend perspectives. Thus in Plate 3, high on both sides, we see 4 men painted on the walls, & in Plate 5 there are four pieces in the form of paintings in the middle of the masonry wall each with its own appropriately-sized circle. In Plates 6, 16, 21, 22, 25, & 28 we find painted canvasses & murals on the sides, and on the lower parts of the walls. In Plates 7 & 27 we  understand they are made in the form of charts. In Plate 19, a tapestry hangs in the middle, in which the doctrines are embroidered. The Plates 5, 8, 14, 17, 18, 20, 22, 25, 26, 27, 28, & 29 likewise have painted walls, but the most important parts are shown alive on the ground or as painting on the wall base, because we have put there the means to see how the position of the swords relates to the lines of the Circle in the form of shadows on the lower line or base. We can see the positions of the blades, on the ground of the circle, by which means the capability to work out the movements of the swords the figures have in their hands becomes quite easy.
-|Because the reader shall find it strange that many of the images are not placed upon the ground, but are above or below the horizon, we think it best they be conceived of as paintings upon the walls; this being because of the unequal circles above the horizon compared to the ground, and for more convenient representation  of the doctrine, & for easier intelligbility in a manner which does not extend perspectives. Thus in Plate 3, high on both sides, we see 4 men painted on the walls, & in Plate 5 there are four pieces in the form of paintings in the middle of the masonry wall each with its own appropriately-sized circle. In Plates 6, 16, 21, 22, 25, & 28 we find painted canvasses & murals on the sides, and on the lower parts of the walls. In Plates 7 & 27 we  understand they are made in the form of charts. In Plate 19, a tapestry hangs in the middle, in which the doctrines are embroidered. The Plates 5, 8, 14, 17, 18, 20, 22, 25, 26, 27, 28, & 29 likewise have painted walls, but the most important parts are shown alive on the ground or as painting on the wall base, because we have put there the means to see how the position of the swords relates to the lines of the Circle in the form of shadows on the lower line or base. We can see the positions of the blades, on the ground of the circle, by which means the capability to work out the movements of the swords the figures have in their hands becomes quite easy.
+| class="noline" | Pource que le ſpećtateur trouveroit eſtrange, que pluſieurs Images ne ſont fixement poſées ſur le fondement, taut au deſſus qu'au deſſoubs de l'Horiſon: nous avons touvé bon de l'advertir, qu'il les faut concevoir comme eſtant deſpeintes aux murailles; cela eſtant fait à cauſe des Cercles inegaux tant au deſſus de l'Horiſon que ſur le plan, pour la repreſentation plus commode de la doćtrine, & pour l'intelligence plus facile du commun qui n'entend les perſpećtives: ainſi au Tableau 3. au deſſus d'un & d'autre coſté ſont deſpeints 4. hommes aux parois, & en la Table 5. il y à quatre pieces en forme de peinture au millieu de la muraille ou maſſonerie, deſquels Cercles chaſcun ſuſſit pour ſoy, & es Tables 6. 16. 21. 22. 25. & 28. au millieu des toilles peinturées, & au coſtez ſont deſpeintes à la paroy, es Tables 7. & 27. faut entendre que cela eſt fait en forme de chartes, & en la Table 19. un tapi tendu ou pendu au millieu, dans leſquel les doćtrines ſont tiſſues, & es Tables 5. 8. 14. 17. 18. 20. 22. 25. 26. 27. 28. 29. de meſme deſpeint aux murailles, mais les premieres pieces ſe demonſtrent plus vivement ſur le fond ou baſe que les autres, car la ſe voit la façon des accords des eſpées & leur operation par les lignes du Cercle; pour ce que en forme d'Eſquierre de la ligne Inferieure ou baſe, on trouve un accord des lames, fait au fond ou Cercle, par lequel le jugement des operations mouvantes des eſpées que les figures tiennent en main, eſt rendu tres-facile.
-|Pource que le ſpećtateur trouveroit eſtrange, que pluſieurs Images ne ſont fixement poſées ſur le fondement, taut au deſſus qu'au deſſoubs de l'Horiſon: nous avons touvé bon de l'advertir, qu'il les faut concevoir comme eſtant deſpeintes aux murailles; cela eſtant fait à cauſe des Cercles inegaux tant au deſſus de l'Horiſon que ſur le plan, pour la repreſentation plus commode de la doćtrine, & pour l'intelligence plus facile du commun qui n'entend les perſpećtives: ainſi au Tableau 3. au deſſus d'un & d'autre coſté ſont deſpeints 4. hommes aux parois, & en la Table 5. il y à quatre pieces en forme de peinture au millieu de la muraille ou maſſonerie, deſquels Cercles chaſcun ſuſſit pour ſoy, & es Tables 6. 16. 21. 22. 25. & 28. au millieu des toilles peinturées, & au coſtez ſont deſpeintes à la paroy, es Tables 7. & 27. faut entendre que cela eſt fait en forme de chartes, & en la Table 19. un tapi tendu ou pendu au millieu, dans leſquel les doćtrines ſont tiſſues, & es Tables 5. 8. 14. 17. 18. 20. 22. 25. 26. 27. 28. 29. de meſme deſpeint aux murailles, mais les premieres pieces ſe demonſtrent plus vivement ſur le fond ou baſe que les autres, car la ſe voit la façon des accords des eſpées & leur operation par les lignes du Cercle; pour ce que en forme d'Eſquierre de la ligne Inferieure ou baſe, on trouve un accord des lames, fait au fond ou Cercle, par lequel le jugement des operations mouvantes des eſpées que les figures tiennent en main, eſt rendu tres-facile.
 |}
@@ Line 339: / Line 348: @@
 {{master begin
-  | title = Book 1 - Tableau/Plate I
+  | title = Book 1 - Tableau / Plates I - XI
-  | width = 100%
+  | width = 60em
 }}
-{| class="floated master"
+{{main|Gérard Thibault d'Anvers/Plates 1-11}}
-! Translation by <br/> [[user:Bruce Hearns|Bruce G. Hearns]]
+{{master end}}
-! Transcription by <br/>[[user:Bruce Hearns|Bruce G. Hearns]]
-|- style="font-family: times, serif; vertical-align:top"
+{{master begin
+ | title = Book 1 - Tableau / Plates XII - XXII
+ | width = 60em
+}}
+{{main|Gérard Thibault d'Anvers/Plates 12-22}}
+{{master end}}
-|Colspan="2"| [[file:Thibault L1 Tab 01.jpg|800px]]
+{{master begin
+  | title = Book 1 - Tableaux / Plates XII - XXII
-[[http://www.geheugenvannederland.nl/nl/geheugen/view/proporties%20menselijk%20lichaam%20verhouding%20tot%20cirkel%20lengte%20degen%20gelle%20johann?query=Girard+Thibault+espee&page=1&maxperpage=36&coll=ngvn&identifier=LEMU01%3A00112044-009 | Large Version]]
+  | width = 60em
+}}
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
+{{main|Gérard Thibault d'Anvers/Plates 23-33}}
-|EXPLANATION OF THE FIRST PLATE
-|DECLARATION DV TABLEAV PREMIER
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|Contents<br>
-The proportions of the body, their relationship to the dimensions of our Circle, and the proper length of the sword.
-|Contenant<br>
-Les proportions du corps de l'homme, rapportées à la figure de noſtre Cercle; & à la iuſte longeur de l'Eſpée.
-|- style="font-family: times, serif; vertical-align:top"
-|A discourse on the superiority & perfection of man, declaring that his body is comprised of  an exact relationship of Divisions, Weights, & Measurements, having movements that relate to the Circle.
-|Diſcours de l'excellence & perfećtion de l'homme, dećlarant que ſon corps eſt exaćtement compaſſé par Nombres, Poids, & Meſures, ayant des mouvements qui ſe rapportent à la figure Circulaire
-|- style="font-family: times, serif; vertical-align:top"
-|Man is the most perfect and most superior of all the creatures in the world, in which is found, amongst the other marks of divine wisdom, such an exquisite representation of the entire universe, in his whole and in his principal parts, that he has been rightly called by the ancient philosophers “microcosm” which is to say, the small world. For beyond the dignity of the soul, which has so many advantanges above all thats is perishable, his body contains a an abridgement, not only of all that we see down here on Earth, but also that which is in Heaven itself. Representing the whole with a harmony so delicate, so beautiful, and complete, and with such concurrence of Divisions, Measures, and Weights, which relates so marvellously to the virtues of the Four Elements, and to the influences of the Planets, that there is no other like it to be found. That most-perfect number Ten continually appears before his eyes, and in its entirety on his digits; and again in two equal halves on his two hands, on each by the number of 5 digits; which are also unequally partitioned by the thumb and by the rest into One and Four, of which the One is composed of two phalanxes, and each the Four of Three: in such fashion this structure has always in view the first and most beautiful Numbers: 1, 2, 3, 4, 5, & 10, which so many illustrious philosophers, like Pythagoras, and Plato, & all those of their schools, held in such esteem, that they sought hide away and so deduce from them the greatest mysteries of their doctrines. As well, we see in the height, width, and thickness of the human body, which has been so precisely measured, that the greatest Architects, both Ancient and Modern, could concieve of no other thing in the world that would make a better basis for the architectural orders than this model, based on man. In this they saw a divine proportion that God Himself  put into the human body, from which they took their inspiration to build, from that time on, into the architecture of Temples, Theaters, Amphitheaters, Palaces, Towers, Vessels, and all other constructions, some of peace, some of war, not just in the whole, but also reflected in the parts: the columns, the peristyles, capitals, pedistals, and other such parts. Thus we read that the Temple of Salomon, this great adornment and miracle of the flourishing Republic of the Jews, was sized according to this same proportion: and what is more, God Himself commanded the Patriarch Noah, upon building of the Ark, to follow the same rule. So that in each one the length is six times the width, and ten times the depth. This is a proportion for which the numbers are always right in front of our eyes, and can be demonstrated clearly on our fingers, where we are accustomed to learning the earliest lessons in natural arithmetic. For this whole sum, which is 10, when multiplied by 3, makes 30 for the depth; and by 5, makes 50 for the width; and multiplied by 10, and by 3 again, makes 300 for the length. These measurements agree with what several noted Authors wrote concerning the same matter. Vitruvius, amongst others, reported the stature of man to be 6 feet measured geometrically. Divide each foot  into 10 degrees, and each degree into 5 minutes, gives 60 degrees and 300 minutes, echoing exactly the three hundred cubits of the Ark. As much as I do not wish to rest so precisely on Vitruvius' authority and accept his geometrical figure of six feet length; it is enough that we can divide the body into six equal measures. Pliny also notes in book 7, chapter 17, that this natural stature of a well-proportioned man accords exactly with the measure of his own arms from the tips of the fingers on one to the end of the other. In summary, all philosophers have made so much of these measurements, and of the proportions of the human body, and have researched so much in one fashion or another that Pythagoras dared declare man as the Measure of All Things. As to the proportion of weight, we cannot doubt that this was also observed with as much art as the numbers or the measurements. All of which is easy to recognize, because man alone, of all the animals, walks upright; in such fashion he holds himself always in counterweight and in balance in all actions, otherwise he would be constantly inconvenienced. For his structure is such, that as each part (except the arms) is higher from the ground, it also increases more and more in weight; so that the lighter and more fragile parts support the other heavier and more robust parts: which would be against Nature and would make it utterly impossible to continue long, in doing so many kinds of movements as we can see performed by the human body, were this not moderated with regard to weight in all the parts from the top of the head to the soles of the feet, in a singular and perfectly artful way. A more complete discussion of this material belongs to anatomists, whose profession is to discuss the particuliarities of this noble structure. We who seek only to explore that which concerns the use of weapons, shall be content to discuss some generalities, notably about the external proportions, so that it shall be much easier to judge the nature and reach of each movement, as we proceed. Since the movements are sometimes made with the whole body, sometimes and more usually with just the arms and hands, and other times with the legs and feet, we shall demonstrate presently that men are capable of performing these necessary and useful movements more easily and promptly than other animals do. What one must know that it is ordinarily, and properly, the job of the arms and hands to carry out the actions of our Will, as use or need requires. The legs and feet serve only to move and turn the body, so as to place the arms and hands so they can properly perform the task we wish to perform where we wish to perform it. Furthermore there is this difference, that the arms and legs are especially suited to perform large movements, whereas the feet and hands perform smaller ones; and as the arms are best used in moves that require strength, the hands are best used in work that requires dexterity. The feet, as pillars that support the body, are, almost immobile when the weight is on the heels, but when on the toes, move quite promptly. Because of this difference, the body can stand firmly by means of the one and yet move and turn swiftly and conveniently by means of the other. From heel to toe, the size of the foot gives him a solid and stable base when he stops, and when he moves, helps to push him forward and give him speed. All parts of the hands are quite agile, and contain, in their width, exactly half the width of the face, which is a quarter of the trunk; the length of the hand is two times the width, and if the hand is closed, the contour of the fist is one third the contour of the trunk: and the hand can naturally act as a small shield, held out in front, either open and extended, or firmly closed. This is why the Jewish author Philo is very right to say that, instead of the natural weapons and defenses of other animals, man was blessed with Reason as his Guide, and Hands as Tools to do as Reason wills; and in that Reason is the Hand of Understanding, the Hand of Reason is the Word, and our hands perform as the Word commands.
-Instruments which have within them all the abilities of the other creatures, and are, consequently, at least equal in greatness, if not superior. This is why man comes into the world deprived of all natural weapons either offensive or defensive, and has but this sole instrument of the hand, by which he may prevail over all. The other animals defend and attack their opponent, one with teeth, another with claws, with hooves, with horns; thus it is wth Elefants, Lions, Bears, Horses, Bulls, Tigers, & other beasts, to whom nature gave each one a single type of natural weapon for their own defence, but to Man, who appears deprived, was blessed with Understanding to know things, Wit to forge things, and Hands to use each and every thing that he can create. In the same way so that he could have even greater advantage, nature gave him, as a special privilege, the power to flex his arms behind and his feet in front at the same time, something impossible for other creatures: and also for the same, or possibly similar reason, the arms were placed in such a way as to be always in view and so help and assist more easily the other parts as they need. So just as the above-mentioned Artists, Architects, Perspectivists, & others have tried to prove the foundations of their rules via the proportions of the human body, so have we navigated the same course, but more adeptly, and have found, with the aid of this same compass, the actual and proportional measure of all Movements, of all the Tempos and Distances necessary to observe in our Training: as it shall be demonstrated in a moment in the description of our Circle; where the measurements and proportions of Man are applied to man himself, and to the movements he makes with his own limbs, from where we derive the aforesaid proportion, and without which it is impossible for him to perform the slightest action in the world. In the practice of swordplay, which I have done for several years, in different countries, and with great experts; of which some come from French schools, others from Italian, and, in sum, each in his own way, I have seen people all over accustom themselves to strange postures, body twisted, feet and hands disjointed out of all natural positions, and in postures inconsistent with the ordinary way in which we walk or stand: such that, instead of evoking through these contortions some sort of power, it impairs and minimizes one's own strength, rather than producing the intended effect. Thus, considering closely, and knowing that in other cases all Arts follow Nature, without ever contravening her, I have chosen to conduct our Training within the same school as this Sovereign Mistress of all good inventions. About which I said at first, that all the Distances and Instances (i.e. steps in the process of fighting) to be observed in training (which are the basic foundations and support for all the following parts) proceed from the proportions of Man, therefore without this same awareness, they cannot be duly comprehended, nor practiced with confidence.
-And the same goes for the Steps and Approaches, short and long, required by the variety of positions  in the performance of these Exercises. From which it is apparent that one must begin with a good knowledge of the proportion of limbs and body parts, that one may at least be able to make some reasonable judgement on the reach of each movement, proportionally to the limb, or limbs, on which the movement depends, and from which it must be continued, ended,  turned, returned, released, bound, or changed in a thousand different ways.
-|L'homme eſt la plus parfaite & la plus excellente de toutes les Creatures du Monde; auquel ſe trouve, parmy les autres marques de la ſageſſe divine, une ſi exquiſe repreſentation de tout l'Vnivers, en ſon entier & en ſes principales parties, qu'il en a eſté appellé à bon droit par les anciens Philoſophes Microcoſme, c'eſt à dire, le Petit Monde. Car outre la dignité de l'ame, qui a tant d'avantages par deſſus tout ce qui eſt periſſable, ſon corps contient un abbregé, non ſeulement de tout ce qu'on voit icy bas en terre, mais encores de ce qui eſt au Ciel meſme; repreſentent le tout avec une harmonie, ſi douce, belle, & entiere, & avec une ſi juſte convenance de Nombre, Meſures, & Poids, qui ſe rapportent ſi merveilleuſement aux vertus des Quatre Elements, & aux influences des Planetes, qu'il ne ſ'en trouve nulle autre ſemblable. Le tres-parfait nombre de Dix luy eſt continuellement repreſenté devant les yeux, en ſon entier ſur ſes propres doigts; & derechef en deux moitiez egales ſur ſes deux mains, à chaſcune par le nombre de Cinq doigts; qui ſont derechef partis inegalement par la poulce, & par le reſte en Vn & Quatre, dont l'Vn eſt compoſé de Deux articles, & les Quatre de Trois: de façon que ceſte ſtructure luy met touſiours en veuë les premiers & plus excellents Nombres 1. 2. 3. 4. 5. 10. dont tant d'Illuſtres Philoſophes, comme Pythagoras, & Platon, & tout ceux de leurs Eſcholes, on fait tant d'eſtime, qu'ils y ont voulu cacher, & en deduire les plus grands myſteres de leur doćtrine. En outre on voit auſi en la longeur, largeur, & eſpeſſeur de ce meſme corps, que les meſures y ſont ſi jusſtement obſervées, que les plus grands Architećts Anciens & Modernes n'ont ſcue choiſir aucune choſe au Monde plus propre pour leur ſervir de regle, ſelon laquelle ils deuſſent former les ordonnances de leurs ouvrages, que ce ſeul patron de l'homme; auquel ils ont remarqué une perpetuelle proportion gardée de Dieu meſme en la fabrique du corps; laquelle ils ont prinſe en exemple, pour façonner à l'advenant les Architećtures des Temples, Theatres, Amphitheatres, Palais, Tours, Vaiſſeaux, & autres Instruments, ſoit de paix, ſoit de guerre, non ſeulement en leur entier, mais auſi en chaſcune des principales parties, Colomnes, Poſteaux, Chapiteaux, Piedeſteaux, & autres membres ſemblables.
-Ainſi lit on, que le Temple de Salomon, ce grand ornement & miracle de la Republique floriſſante de Iuifs, a eſté compaſſé ſelon ceſt meſme proportion: Et qui plus eſt, que Dieu meſme auroit commandé au Patriarche Noë, en baſtiſſant l'Arche, d'enſuivre la meſme regle. Car tout ainſi que le corps de l'homme contient 300 minutes en longeur; 50 en largeur; & 30 en eſpeſſeur par le milieu de la poitrine: auſſi pareillement l'ordonnance de l'Arche a eſté faite à 300 coudées de longeur; 50 de largeur; & 30 de hauteur: de ſorte qu'en l'un & en l'autre la longeur eſt ſix fois autant que la largeur, & dix fois, que la profondeur. Qui eſt une proportion, donc nous avons touſjours devant nos yeux les nombres, & les pouvons nous demonſtrer clairement ſur nos doigts, où nous avons couſtume d'apprendre les premieres leçons de l'Arithmetique naturelle.
-Car la ſomme entiere, qui en eſt 10, eſtant multipliée par 3, fait 30 pour l'eſpeſſeur; & par 5, fait 50 pour la largeur; & multipliée par 10, avec le redouble de 3, fait 300 pour la longeur. Et à ces meſures s'accorde auſſi ce que pluſieurs graves Auteurs eſcrivent en touchant la meſme matiere: comme entre autres, que Vitruve a rapporté la ſtature de l'homme à 6 pieds de meſure Geometrique; le pied à 10 degrez; & chaſque degré en 5 minutes; qui font 60 degrez, & 300 minutes, retirants juſtement aux trois cents coudees de l'Arche.
-Combien que je ne veuille pas m'arreſter ſi preciſement ſur l'authorité de Vitruve, à luy donner ſix pieds Geometriques de longeur; ce m'eſt aſſez qu'on la puiſſe partir en ſix meſures égales. Pline remarque auſſi livre 7. chapitre 17. que ceſte ſtature naturelle de l'homme bien proportionné s'accorde exaćtement à measure de ſa propre braſſee, depuis le bout des doigts de l'une des mains juſques au bout de l'autre. En ſomme touts Philoſophes ont fait tant d'eſtime de ceſte meſure, & de la proportion de ce corps humain, & l'ont tant recerchée, les uns d'une façon, les autres de l'autre, que Pythagoras a oſé nomme l'homme La Meſure de tout. Quant à la proportion des Poids, il ne faut pas douter, qu'elle n'y ſoit auſſi obſervée avec tout autant d'artifice, que les Nombres, ou les meſures. Ce qui eſt aiſé à cognoiſtre, par ce qu c'eſt l'homme ſeul de touts les animaux qui marche droit; de façon qu'il ſe tient touſiours en contrepoids & en balance en toutes aćtions, autrement il en ſeroit à touts moments incommodé.
-Car ſa ſtrućture eſt telle, que touts ſes membres (exceptez le bras) à meſure qu'ils ſont plus relevez de la terre, auſſi ſont ils plus peſants de plus en plus; ſi que les parties plus legeres & plus foibles ſoutiennent les autres plus peſantes & plus robuſtes: qui ſeroit choſe contre Nature & du tout inſupportable pour continuer longuement, en tant & en ſi diverſes ſortes de mouvements, comme on voit que ce corps humain pratique, s'il n'eſtoit moderé au regard du Poids en toutes ſes parties depuis le ſommet de la teſte juſqu'aux plantes des pieds, d'un ſingulier & parfait artifice. La declaration plus ample de ceſte matiere appartient aux Anatomiſtes, qui font profeſſion de declarer les partiularitez de ceſte noble ſtrućture: nous qui ne pretendons que d'en expoſer ſeulement ce qui touche l'exercise des Armes, ſerons contents d'en declarer quelques choſes en gros, notamment touchant les proportions exterieures; afin q'il ſoit par cy apres d'autant plus facile à juger de la nature & portee de chaſcun des mouvemēts, qui en procedent. Puis donc que les mouvements ſe font quelques fois avec le tronc entier du corps, quelquesfois & plus ſouvent avec les bras & les mains, & autres fois avec les jambes & les pieds, nous demonſtrerons preſentement, que les hommes ſont capables d'exploiter leurs movemēts neceſſaires & utils en plus grand nombre & plus aiſeement & plus promptement, que ne font les autres animaux. Dont il faut ſçavoir, que c'eſt ordinaire & proprement l'office des bras & des mains d'executer le commandement de la volonté, en faiſant les aćtions que l'utilité ou la neceſſité demande; & que les jambes & les pieds ne ſervent communement à autre choſe, au'à tranſporter et à tourner le corps, & à mettre le bras & mains en places, où la Volonté pretend quel execution ſoit fait: & d'avantage qu'il y a ceſte difference, que les bras & les jambes ſont ſpecialement propres à faire les grands mouvements, ainſi que les pieds & les mains ſont propres aux moindres: & comme les bras ſont particulierement capables à executer ce où il faut de la force, ainſi les main le ſont d'autrepart pour travailler avec dexterité. Les Pieds, comme pilliers qui ſouſiennent le corps, ſont devers les talons quaſi immobiles, mais devers les orteils ils ſe mouvent aſſez promptement: de ſorte quepar l'inegalité de ceſte ſtrućture le corps ſe peut affermir deſſus, au moyen de l'un, comme il ſe peut d'autrepart remuer & tourner viſtement & commodement de touts coſtez, au moyen de l'autre. En l'un & en l'autre derechef il reçoit un grand ſoulas par la juſte longueur, qui luy fournit un fondement ſtable & ſolide quand il s'arreſte; & quand it marche, elle aide à le pouſſer & luy donner ſa courſe. Les Mains ſe meuvent fort agilement en toutes leurs parties, & contiennent en leur plus large la juſte moitié de la largeur du viſage, qui eſt le quart au regard de la poitrine: la longueur en eſt deuz fois autant: & eſtant la main fermée, le contour du poing ſera le tiers du contour de la poitrine: en ſorte qu'elle luy peut naturellement ſervir d'eſcuſſon pour la defendre, en la tenant devant, ſoit ouverte et eſtendue, ou bien ſoit fermée.
-Ceſt pour quoy Philo, autheur Iuif, a tres-bien rencontré à dire, qu'au lieu de touts les ornements & defenſes naturelles des autres animaux, l'homme a eſté doué de la Raiſon, comme Direćtrice, & de Mains, comme Inſtruments pour executer ce qu'elle veut: & que la Raiſon eſt la Main de l'Entendement; la main de la Raiſon c'eſt la Parole; & les Mains corporelles celles qui font l'execution de ce que la Parole commande. Inſtruments, qui contiennent en eux toute la ſuffiſance des autres, & qui par conſequent les egalent en dignité, voire les ſurmontent. Pour laquelle cauſe il vient au Monde deſpourveu de toutes armes, tant offenſives que defenſives, & n'a que ce ſeul inſtrument de la main, au moyen duque il ſe puiſſe prevaloir de toutes. Les autres animaux ſe defendent & offenſent leurs contraires, l'un avec les dents, l'autre avec les ongles, les pieds, les cornes; ainſi quil ſe voit és Elefans, Lions, Ours, Chevaux, Taureaux, Tigres, & autres beſtes, à qui la Nature a departiaſſez chichement une ſeule eſpece d'Armes a chaſcune, pour la neceſſité de leur defenſe; mais à l'homme, qui en ſemble eſtre du tout privé, en recompenſe elle l'a doüé d'Entendement pour les cognoiſtre, d'Eſprit pour les forger, & de Mains pour s'en aider de toutes & telles qu'il en puiſſe eſtre. meſme afin qu'il s'en peuſt aider avec plus d'avantage, elle luy a donné par ſpecial privilege de pouvoir à meſme inſtant fleſhir les bras en arriere & les pieds en avant, choſe impoſible aux autres creatures: comme auſsi pour la meſme, ou pour ſemblable cauſe, la ſituation naturelle des bras a eſté placée en tel endroit, que les operations des mains fuſſent touſiours ſous le gouvernement de la veuë, pour en ſecourir & aſsiſter tand plus aiſement le reſte des membres en leurs neceſsitez. Tout ainſi donc que le ſuſdits Artiſtes, Architećtes, Perſpećtiviſtes, & autres on taſché de prouver les fondements de leurs regles par les proportions du corps de l'homme, ainſi avons nous pareillement tenu la meſme courſe, mais avec meilleure adreſſe, & avons trouvé à l'aide de ceſte meſme buxole la vraye & proportionelle meſure de touts les Mouvements, de touts les Temps, & Diſtances, neceſſaires à obſerver en noſtre Pratique: comme il vous ſera demonſtré tout à l'inſtant en la declaration de noſtre Cercle; où les meſures & proportions de l'homme ſont appliquées à l'homme meſme, & aux movements qu'il fait avec ſes propres membres, où ladite proportion ſe trouve, & ſans laquelle il luy eſt impoſſible de faire la moindre aćtion du Monde. En pratiquant donc ceſt Exercice, comme i'ay fait par pluſieurs annees, en divers pays, & avec de grands amateurs; dont les uns tiroyent à la Françoiſe, les autres à l'Italienne, & en ſomme chaſcun à ſa mode; j'ay veu qu'on s'accouſtume par tout à des poſtures eſtranges, le corps plié en pluſiurs courbures à pieds & jambes diſioinćtes hors de proportion naturelle, & en ſituations du tout repugnantes à la mode ordinaire qu'on tient en cheminant ou en demeurant ferme: de ſorte qu'au lieu de faire paroiſtre par ces mines quelque grand courage, on s'incommode & amoindrit on ſes propres forces, pluſtoſt que d'en obtenir l'effećt de l'intention pretendue. Ce que conſiderant de pres, & ſachant d'autrepart, que touts les Arts enſuivent la Nature, sans jamais y contrevenir, j'en ay prins occaſion de vouloir conduire auſsi noſtre Exercise à la meſme Eſchole de ceſte Souveraine Maiſtreſſe des bonnes inventions.  En quoy j'ay remarqué premierement, que toutes les Meſures & Inſtances à obſerver en ceſt Pratique (qui ſont les premiers fondements & l'appuy de toutes le parties ſuivantes) procedent de la proportion du corps de l'homme, comme auſsi ſans la meſme cognoiſſance elles ne ſçauroyent eſtre deuemēt comprinſes, non plus que d'eſtre pratiquées avec aſſeurance. & qu'auſsi le ſemblabe en eſt il de Pas & Demarches ordinaires ou extraordinaires, que l'uſage de l'Exercise & la varieté des occaſions requierent. Par où il appert, qu'il faut entrer ſi avant en ceſte cognoiſſance de la proportion des membres & parties du corps humain, qu'on puiſſe à tout le moins faire quelque raiſonnable jugement de la portée de chaſcun mouvement, à proportion du membre ou des membres, d'où il depend, & desquels il doit eſtre continué, fini, tourné, retourné, laſché, bandé, ou changé en mille & mille manieres.
-|- style="font-family: times, serif; vertical-align:top"
-|The first thing to know is that the philosophers attibuted to the microcosm of the human body various figures, of which we will later discuss the triangle, the quadrangle, and the pentagon. For the moment, we shall say the figures made by the body are also round or circular, in accordance with Hippocrates, Prince of Doctors, who said that the body is a circle. Which can be understood as much in regard to the actions and operations of its interal parts, and their attendent functions, so reciprocal and each following one on the other, so we can find no beginning and no end,  as if following the circumference, as it can be also to movements of his limbs which always go around, from the strength of the centre to the weakness of the extreme circumference. Thus, as it is now time to turn to the question of, and to discuss, Range, which is appropriately proportional to stature, position, approaches, and generally all external movements of this same body, I now introduce our Circle, which, as I say, contains all the above-mentioned qualities, and is taken from the correct measurements and proportions of a man. All mathematicians know that the circle or round figure is the simplest, primary, and moreover most perfect, superior, and most useful of all for defense; a figure which has only one point of contact on its surface at only one point at a time: thus such a noble thing as our body cannot help but make use of such a useful figure: to which also can be demonstrated in many ways and principally on the long extension; which is, when standing straight upright, feet joined, and the arms extended directly above, so that the elbows are by the top of the head. For when he holds himself thusly, either upright beside a wall, or extended in the same  way on the ground, and we place one branch of a compass on his navel, and the other on his fingernails or at the soles of his feet, and we draw about him a circumference, we create a circle of which the centre will be on the person's navel, the Diameter will be the person's extended height, and the circomference will touch, on one side, the soles of the feet, on the opposite, the tips of the fingers. If one finds it does not fit, the body has not been exactly positioned following the rules of composition. Thus the Circle, which we intend to use throughout this book to perform our exercises, which is proportional to all the movements we shall make, with arms, and legs, and the body as a whole. One could draw still other Circles from man's proportions in many ways (such as putting the Centre on the shameful parts and draw the Circumference at the top of the head and the soles of the feet) but these cannot suffice, nor have the convenient measure we are looking for, because they have no relation to the proportions of the extended arms, which is the principal aspect required for this Training, which is why, together with certain other considerations with respect to the question of using the Circle, we must use the extended length as an exact measure for the Diameter, and not any other.
-|Il faut donc ſçavoir pour le premier, que les Philoſophes attribuent à ce Microcoſme du corps humain diverſes figures, dont it ſera parlé autrement de la triangulaire, quadrangulaire, & pentagone. Preſentement nous diſons, qu'il eſt auſſi rond ou circulaire en la figure de ſes mouvements, à quoy s'accorde le dire d'Hippocras Prince de Medecins, que le corps eſt un Cercle. Ce qui ſe peut entendre tant au regard des aćtions & operations naturelles de ſes parties interieures, & de leurs alterations ſubalternes, tellement reciproques & ſuccedantes les unes aux autres, qu'il ne s'y trouve non plus de commencement ne de fin, qu'en la rondeur d'une circonference, auſſi ſe peut il rapporter à la figure de touts ſes mouvements locaux, qui va touſiours en rond, s'eſtendant depuis le centre de ſa force juſqu'à l'extreme circonference de ſa foibleſſe.
-Or puis qu'il eſt donc preſentement queſtion, de vous faire voir la Meſure, qui ſoit convenable & proportionée à la ſtature, ſituations, demarches, & generalement à touts les mouvements exterieurs de ce meſme corps, voicy la figure de noſtre Cercle, que nous diſons contenire toutes les ſuſdites qualitez, & eſtre tiré de la propre meſure & proportions du corps de l'homme. Touts les Mathematiciens ſçavent, que la figure circulaire ou ronde eſt la plus ſimple, la permiere, voire auſſi la plus parfaite, la plus excellente, & la plus capable de toutes pour la defenſe; comme celle qui ne ſe laiſſe toucher en la ſurface, qu'en un ſeul point à la fois: dont une figure ſi accomplie ne devoit pas manquer à un corps ſi noble: auquel auſsi elle peut eſtre demonſtrée in diverſes manieres; & principalement ſur la longeur eſtenue; ceſt à dir quant il ſe tient droit ſur ſes jambes, à pieds joinćts, & les bras éſtendus droitement en haut, tellement que les coudes luy egalent le ſommet de la teſte. Car lors qu'il ſe tient en telle ſituation, ſoit debout contre un mur, ſoit eſtendu en la meſme ſorte par terre, & qu'on luy mette l'une des branches d'un grand compas ſur le nombril, & l'autre ſur les orteils ou contre la plante des pieds, & qu'on en tire en rond une circonference, il en ſourdra un Cercle; dont le Centre ſera ſur le nombril de la perſonne, le Diametre en ſera comme la hauteru eſtendue, & la Circonference en touchera d'un coſté la plante des pieds, & à l'oppoſite les bouts des ſes doights. Si on y trouve de la faute, le corps n'a pas eſté exaćtement proportionné ſuivant les regles de ſa compoſition. Or voilà maintenant le Cercle, duquel nous pretendons uſer en tout ce Livre pour l'adreſſe de noſtre Exercice: lequel, d'autant qu'il eſt proportionné à touts le mouuements qu'il ſçauroit faire, avec bras & jambes, & avec tout le corps entier, ou avec chaſcune de ſes parties. On pourroit tirer encor d'autres Cercles de ceſte proportion de l'homme en diverſes manieres (comme en mettant le Centre ſur les parties honteuſes, & la Circonference au  ſommet de la teſte & à la plante des pieds.) mais iceux ne peuvent avoir la meſme ſuffiſance, ne la convenance des meſures que nous cherchons preſentment; à raiſon qu'ils n'ont pas de proportions avec les bras eſtendus, auxquels il appartient en ceſt Exercice d'executer la principale partie de la beſoigne: pour laquelle cauſe, enſemble auſsi pour quelques autres conſiderations, s'il eſt question de ſe ſervir icy de Cercle, il n'y faut advouer autre meſure de Diametre, que celle qui s'accorde exaćtement avec ceſte longeur eſtendue.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|HERE FOLLOWS THE METHOD
-of drawing upon the floor, the Circle and all its components
-|S’ENSVIT LA MANIERE DE<br>
-covcher le cercle svr le plan, avec tovtes ses appartenances
-|- style="font-family: times, serif; vertical-align:top"
-|Having shown the dimensions of the Diameter, Centre, and Circumference, it now follows that we describe the rest; to find the proportions on which the circle depends: and to this end, must, of necessity, enscribe the entire Circle on a smooth floor, in its appropriate size, using as the measure of the diameter, the extended length of the person who shall do the moves. This is how to proceed.
-|Ayant monſtré la dimenſion du Diametre, le Centre, & la Circonference, il s'enſuit maintenant que nous declarions auſſi le reſte; pour venir apres aux proportions qui en dependent: & à ceſte fin, faut neceſſairement deſcrire le Cercle entier ſur un plan bien uni en ſa juſte & convenable grandeur, en prenant la meſure du diametre ſur la longeur eſtendue d'une perſonne, au corps de laquelle on voudra faire les preuves. Or voicy comme il y faudra proceder.
-|- style="font-family: times, serif; vertical-align:top"
-|Choose an appropriate place, with a flat, solid floor, on which you shall first mark the ''Centre'' point with chalk, in the location most suitable for training.
-|Choiſiſſiz un lieu propre, ou il y ait un plancher bien uni, ſur lequel vous marquerez pour le premier avec de la croye le poinćt du ''Centre'', en tel endroit qui vous ſemblera plus commode.
-|- style="font-family: times, serif; vertical-align:top"
-|This done, take a sword of one half-diameter length, so that when the tip is placed upon the ground between the person's two feet, the crosspiece of the hilt will come just to the height of the navel, and place one of the ends of the crosspiece on the centre point; and use the tip to draw the circle by holding a piece of chalk in your fingers, thus describing the ''Circumference''.
-|Cela fait, prenez une eſpee de la longeur du demi-diametre, telle que la poinćt eſtant miſe en terre entre les deux pieds de la perſonne, les branches de la garde luy viennent juſtement à la hauteur du nombril: & en mettez l'une des branches ſur le poinćt du centre; & laiſſez mener la poinćte à un ſecond avec un morceau de croye entre les doigts en rond, deſrivant ainſi la ''Circonference''.
-|- style="font-family: times, serif; vertical-align:top"
-|This being drawn, take a chalked carpenter's cord, and snap the ''Diameter'' according to the most suitable use of the space, extending both ends two feet (60 cm) beyond the circumference: and label these two crossing-points of the Circumference; the one below the centre with a C, and the other, opposite, with an X.
-|Laquelle eſtant tracée, prenez une cordelle à la mode des charpentiers, que vous frotterez avec de la croye, & en couchez le ''Diametre'' ſelon la commodité de la place, le prologneant à toutes ſes deux extremitez de la longeur de deux pieds outre la circonference: & marquerez les deux coupures de la Circonference; celle qui eſt par decà le Centre, d'un C, & L'autre, à l'oppoſite, d'un X.
-|- style="font-family: times, serif; vertical-align:top"
-|Next, through the Centre, draw a perpendicular line across, which shall be the ''Perpendicular Diameter'', each of the two ends likewise passing two feet beyond the circumference: and also label both of these crossing-points of the Circumference with an N.
-|Menez apres en la meſme ſorte par le Centre une ligne coiſiere & perpenduculaire, qui ſera le ''Diametre perpendiculaire'', outrepaſſant pareillement de ſes deux bouts la Circonference à deux pieds de longeur: & marquez encor ſemblablement les deux coupures de la Circonference, chaſcune d'un N.
-|- style="font-family: times, serif; vertical-align:top"
-|To find this Perpendicular Diameter, first put the tip of the sword on the letter C and one of the arms of the crosspiece along the circumference.
-|Pour trouver ce Diametre perpendiculaire, mettez premierement la poinćte de l'eſpee ſur la lettre C. & l'une des branches de la croiſee ſur la Circonference,
-|- style="font-family: times, serif; vertical-align:top"
-|Using the crosspiece as a pivot, move the tip 180 degrees away from C and, again using the tip, draw an arc outside the circle.
-|menant derechef la poinćte circulairement en avant, & en deſcrivant ſur le ſeuil au dehors de la circonference un arc, reſpondant en droite ligne à la lettre C par le poinćte de l'attouchement de la branche.
-|- style="font-family: times, serif; vertical-align:top"
-|Do the same, starting from the letter X, so the two arcs cross each other.
-|Ce qu'il faudra faire auſſi pareillement en commenent par la lettre X, dont le ſuſdit arc ſera coupé en croiſade d'un autre ſemblable.
-|- style="font-family: times, serif; vertical-align:top"
-|This cross will act as a guide for drawing the perpendicular diameter, by taking the cord from there and through the centre beyond the circumference to the opposite side.
-|Ceſte croix vous ſervira de guide à tirer le Diametre perpendiculaire, en menant la cordelled par icelle & par le centre outre la circonference do coſté oppoſite.
-|- style="font-family: times, serif; vertical-align:top"
-|Once again, place one end of the crosspiece on each of the four letters C, N, X, & N in turn, and, with the tip, draw arcs just outside the circumference between the four letters, thus marking four crossing-points, which will be the guide-points for the two ''Oblique Diameters''.
-|Mettez apres derechef la croix de l'eſpee avec l'une des branches ſur chaſcune de ces quatre lettres C.N.X.N. & en faites tirer avec la poinćte dehors le Cercle à chaſcune deux arcs, reſpondants l'un à l'autre en droite ligne par leſdits lettres: dont il fourdra quatre croiſades, qui donneront l'adreſſe pour couche les deux ''Diametres obliques''.
-|- style="font-family: times, serif; vertical-align:top"
-|Again, in the same way, place the crosspieces on the ends of the Oblique Diameters, mark outside the circle where the tip crosses the extensions both the Principal and Perpendicular Diameters. These marks define the terminals of the lines beyond the circle, the ends of which are labelled with letters; the one below C with A; the one opposite with Z; the two others with O.
-|Tirez lors derechef en la meſme ſorte des arc dehors le Cercle ſur les quatre bouts de ces deux Diametres obliques, deux & deux pour chaſcun poinćt, allants par les ''Diametres prolongez'' principal & perpendiculaire. Ces arcs ſeront les bornes des parties adjoinćtes, dont les extremitez ſeront marquées de lettres; celle qui eſt deſſous le C, d'un A; & à l'oppoſite d'un Z; les deux aures chaſcune d'un O.
-|- style="font-family: times, serif; vertical-align:top"
-|From these four points, we draw the ''Outside Square'', drawing lines from A to O on the right & left sides and likewise from Z to O.
-|Sur ces quatre poinćts ſera tiré le ''Quarré circonſrit'', en menant une ligne de l'A juſques à l'O à droite, & une autre pareillement à gauche; puis ſemblablement deux autres, l'une à droite, & l'autre à gauche depuis le Z juſqu'au deux O.
-|- style="font-family: times, serif; vertical-align:top"
-|Using the points C, N, X, & N, you will draw the ''Inside Square'', as well as the four ''Quadrangles''; draw the line on the right hand side through C and N from one edge of the Outside Square to the other and another to the left side. Label the mid-points, where these lines cross the Oblique Diameters with a G. Next draw two more similar lines through the points X & N on the left & right sides and label the mid-point of each of these lines with an S.
-|Ce fait par les quatre poinćts C. N. X. N. vous deſcrirez le ''Quarre Inſcrit'', enſemble avec les quatre ''Quadrangles''; en menant une ligne à main droite par le C & par l'N, ſur les coſtez oppoſites du Quarré circonſcrit; puis encor une autre pareille à main gauche; & puis deux autres par les lettres X & N, l'une à droite, & l'autre à gauche, leſquelles lignes faudra marquer ſur les poinćts du mitan, qui ſont coupez par les Diametres obliques, entre les deux lettres C. & N. à chaſcun des coſtez deſſous le Centre d'un G; & deſſus au mitan des lettres N. & X. à chaſcun des coſtez d'un S.
-|- style="font-family: times, serif; vertical-align:top"
-|Then draw two ''Interior Collaterals'' through C & S to the left and right.
-|Apres tirez par les lettres C. & S. deux ''Collaterales Interieures'', l'une à droite, & l'autre à gauche.
-|- style="font-family: times, serif; vertical-align:top"
-|Likewise draw two more through the letters X & G.
-|Semblablement tirez en deux autres par les lettres X & G.
-|- style="font-family: times, serif; vertical-align:top"
-|Then draw two ''Interior Transverses'' on the right hand side above the Centre from the letter N across the Diameter line through S and below the centre across the Diameter through G.
-|Apres deux ''Traverſantes Interieures'' par la lettre N. à main droite; l'une par deſſus le Centre par l'S; & l'autre au deſſous par le G oppoſite.
-|- style="font-family: times, serif; vertical-align:top"
-|Likewise draw two more in the same way through the same letters from the opposite side.
-|Semblablement encor deux autres, à tirer en la meſme ſorte & par les meſmes lettres du coſté oppoſite.
-|- style="font-family: times, serif; vertical-align:top"
-|This done, label the four sides of the Outside Square in the following manner. First the side A-O on the right hand side. From A, label the first angle of the quadrangle with B; label the end of the Interior Collateral that passes through G below the oblique diameter, with D; label the end of Interior Traverse that passes through the same point G, with F; label the angle of the quadrangle at O-N, with K.
-|Ce qu'eſtant fait, il faudra marquer de lettres les quatre coſtez du quarré circonſcrit, en la maniere suivante. Premierement le coſté A O à main droite de la figure. Sur l'angle du Quadrangle ſoit eſcrit un B: ſur la fin de la collaterale interieure qui vient par le G en deçà le Diametre oblique, un D: ſur le bout de la traversante interieure, qui passe à travers le mesme poinćte, un F: & sur l'angle du prochain quadrangle, un K.
-|- style="font-family: times, serif; vertical-align:top"
-|After that, on the two other sides O-Z, begin again on the right side; label the angle of the quadrangle O-N with P; label the end of the Interior Transverse through S that ends before the Oblique Diameter, with T; label the end of the Interior Collateral through S that ends just beyond that, with W; label the angle of the Quadrangle Z-X, with a Y. Then do likewise on the left hand side.
-|Les meſmes lettres ſeront auſſi marquées A O, à main gauche.
-Label the same letters along the line A-O on the left hand side.
-En apres ſur les deux autres coſtez O Z, commencez derechef à droite; & mettez ſur l'angle du Quadrangle O N, un P: sur le bout de la traverſante, qui ſe finit en deçà le Diametre oblique, un T: sur la collaterale, qui finit au delà, W: sur l'angle du dernier Quadrangle, un Y. Et en ſoit fait paraillement le meſme à l'autre coſté, qui est à main gauche.
-|- style="font-family: times, serif; vertical-align:top"
-|After this, trace two ''Exterior Transverse'' lines, one on the right hand side, the other on the left, from D, across the Principal Diameter, through G opposite.
-|Apres il faudra tracer deux ''Traverſantes exterieures'', l'une à main droite, & l'autre à gauche, allants depuis les D, par le Diametre principal, & par les G opposites.
-|- style="font-family: times, serif; vertical-align:top"
-|Likewise draw two more in the upper half of the circle from W, across the centre, through S opposite.
-|En ſemblable encor deux autres en la partie ſuperieure du Cercle, depuis les W. par le Diametre, & par les S oppoſites.
-|- style="font-family: times, serif; vertical-align:top"
-|Similarly on the right side of the Circle, draw two ''Exterior Collaterals'' one from the side A-O, through G, to T;  & the other from F through S, out to the side O-Z.
-|Pareillement auſſi en la partie droite du Cercle deux ''Collaterales exterieures'', à mener, l'une du coſté droit A O, par le G, juſques au T: & l'autre à tirer de l'F, & à continuer par l'S, juſques au coſté droit de la partie ſuperieure du Quarré circonſcrit.
-|- style="font-family: times, serif; vertical-align:top"
-|Likewise also, draw two others on the left side of the figure in the same way.
-|Semblablement encor deux autres en la partie gauche de la figure, à tracer en la meſme ſorte.
-|- style="font-family: times, serif; vertical-align:top"
-|Thus we have drawn all the lines within the Circumferance. Label each double-cut (except the Centre), with the following letters. Along the Principal Diameter label the first cross-cut line above C with E; label the second with H; label the third, beyond the centre, with R; label the fourth with V. There are, likewise, four sections along the Perpendicular Diameter; the two closest to the centre labelled L, & the two others each labelled M. Where the Interior Collateral lines cross the oblique diagonals and the Interior Transverse line, label the lower ones (near H) with I and the upper ones (near R) with Q.
-|Et par ainſi voilà achevées toutes les lignes, qui entrent dans le pourpris de la Circonference, ſur leſquelles il faudra mettre à chaſque double entrecoupure de lignes (excepté le Centre) les lettres ſuivantes. Premierement ſur le Diametre principal, à la permiere entrecoupure apres le C, il faut un E: à la seconde, un H: à la troisieme, qui est par delà le Centre, un R: & finalement à la quatrieme, un V. Sur le Diametre perpendiculaire y a pareillement quatre sećtions; dont les deux plus proches du Centre porteront, chaſcune un L: & les deux autres, chaſcune un M. Aux doubles entrecoupures de chaſcune des collaterales interieures par deça le Centre, mettez à chaſune un I. & aux autres qui sont par delà, un Q. à chaſcune.
-|- style="font-family: times, serif; vertical-align:top"
-|As to the lines outside the Circumference, first draw in each of the Quadrangles its ''Diagonal'', across the Extended Diameters, from B to B, from Y to Y, and from K to P.
-|Quant aux lignes qui demeurent hors de la Circonference, tirez premierement à chaſcun des Quadrangles ſa ''Diagonale'', à travers les Diametres prolongez, de B à B: de Y à Y: & de K à P, dans les deux Quadrangles opposites de main droite & gauche.
-|- style="font-family: times, serif; vertical-align:top"
-|Second, draw a Foot-Line or ''Pedal Line'' across these same Quadrangles between the end-points of the Collateral lines and between the end-points of the Transverse lines.
-|Secondement tirez dans ces meſmes Quadrangles, du bout de l'une des lignes collaterales au bout de l'autre, à chaſcun une ligne de pied, ou ligne ''Pedale''.
-|- style="font-family: times, serif; vertical-align:top"
-|And finally, add the lines we shall call the length & width of the Square Extension.
-|Et finalement adjouſtez y celles que nous apellerons les ''longeur & largeur des Eſquierres''.
-|- style="font-family: times, serif; vertical-align:top"
-|First, to fit the lengths, pass the cord through the centres of two nearest Quadrangles; trace a line from the end of the Foot-Line to where the cord crosses the circumference; likewise trace a line opposite from the circumference to the end of the other Pedal Line. Do this all around the Circumference.
-|Pour adjuster permierement les longeurs; compassez voſtre cordelle par les centres de deux prochains Quadrangles; & tracez en ceſte ſorte une ligne de longueur depuis le bout de la ligne de Pied juſques à la circonference du Cercle; & en ſemblable tracez en encore une autre à depuis la circonference juſques au bout de l'autre ligne Pedale. & voilà comme il en faudra faire tout alentour de la Circonference.
-|- style="font-family: times, serif; vertical-align:top"
-|To fit the widths of the Square Extensions (these lines stay outside the edges of the Quadrangles) pass your cord on the ends of one Exterior Collateral Line and one Exterior Transverse Line on the ends which are not labelled with letters, & trace two lines of width, one below the other beyond the Circle, again going all around the Circumference.
-|Pour adjuſter les Largeurs des Eſquierres, (ce ſont les lignes qui demeurent au dehors aux coſtez des Quadrangles) compaſſez voſtre cordelle ſur les bouts d'une Collaterale & d'une Traverſante exterieure, aſſavoir ſur les bouts qui ne ſont point marquez de lettres, & tracez en ceſte ſorte deux lignes de largeur, l'une deçà & l'autre delà, en la meſme façon que vous venez de faire le Longueurs, en allant derechef tout à l'entour de la Circonference.
-|- style="font-family: times, serif; vertical-align:top"
-|This, in sum, is the way to lay out this plan for our Training, simple & easy, but in any case most useful if it is drawn very carefully. Meanwhile I would advise, if you do not have a sword of the correct length of a radius with which to draw the circumference, and subsequently the arcs for the cross-points to position the Diameters and the Outside Square, that in that case you can use the cord, pinning it to the Centre, to draw the Circonference & the rest. However, nothing is as sure as the sword itself, with its solid blade that will not stretch and will remain the same length. Otherwise faults could be introduced.
-|Voilà en ſomme la mode d'accommoder le Plan de ceſtuy noſtre Exercice, ſimple & facile, mais par adventure plus utile que ſi elle ſuſt dreſſée fort curieuſement. Cependent je vous aviſe, ſi c'eſt que vous n'ayaez point d'eſpee de ceſte juſte longeur du demi-Diametre pour en tirer la Circonference, & conſequemment les croiſades des arcs pour l’adreſſe des Diametres, & du Quarré circonſcrit; qu'en ce cas vous vous ſerviez de la cordelle, l'attachant en poinçon fiché sur le poinćt du Centre, pour en tirer en rond ladite Circonference,  & le reſte à l'advenenant: toutesfois il n'eſt rien plus ſeur que l'eſpee meſme, qui demeure jouſiours immobile en une meſme longueur, par la ſolidité de la lame: de ſorte que malaiſement y peut il avenir de la faute.
-|- style="font-family: times, serif; vertical-align:top"
-|Now, to clarify this material, here follows a catalogue of the names of the lines, so that the reader may have a reference to the Plate of all the lines and figures of this Circle which are needed for practical use.
-|Maintenant afin que ceſte Matiere ſoit un peu eſclaircie, & que le Lećteur puiſſe avoir devant ſes yeux une Table de toutes les lignes & figures de ce Cercle, qui sont neceſſaires à observer en l’uſage de la Pratique, nos en metrons icy le Catalogue.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|LIST AND NAMES OF ALL THE LINES AND FIGURES OF THE CIRCLE, NEEDED FOR PRACTICAL USE
-|DENOMBREMENT ET APPELATIONS DE TOVTES LES LIGNES ET FIGVRES DV CERCLE, NECESSAIRES A OBSERVER EN LA PRATIQUE
-|- style="font-family: times, serif; vertical-align:top"
-|The whole figure is called the Circle : because the circle forms the base on which all the other parts depend and remains the principal subject, the foundation of all the rest with regard to the Training, as they appear hereafter, as to the proportions and measures of Man.
-|La figure entiere ſera appellée ''Cercle'': pource que c'eſt du Cercle qu'elle depend en ſon entier & en toutes ſes parties; iceluy Cercle en demeurant le ſujet principal, voire le fondement de tout le reſte, tant au regard de l'Exercice, comme il paroiſtra cy apres, qu'au regard des proportions & des meſures du corps de l'homme.
-|- style="font-family: times, serif; vertical-align:top"
-|''Centre'' is the point in the middle of the Circle.
-|''Centre'' c'eſt le point du milieu du Cercle.
-|- style="font-family: times, serif; vertical-align:top"
-|''Circumference'' is the round line that forms the Circle.
-|''Circonference'' c'eſt la ligne rond qui fait le Cercle.
-|- style="font-family: times, serif; vertical-align:top"
-|C-X is the ''Diameter''. In truth, there are four Diameters found in this figure; However to avoid confusion, it is necessary to distinguish between them. This is why I have left the general term Diameter to this which is the principal one in the Training: such that I even refer to the parts beyond the circumference as the Diameter, from the letter A to Z.
-|C X. Eſt le ''Diametre''. Il eſt vray, qu'il ſe trouve quatre Diametres en ceſt figure; toutes fois pour eviter confuſion, il eſt neceſſaire qu'ils ſoyent diſtinguez. C'eſt pourquoy nous avons laiſſé le nom general de Diametre, à ceſtuy-cy qui eſt le principal en l'Exerciſe: de ſorte que nous l'appellons meſme Diametre en ſes parties adjouſtées au dehors de la circonference, depuis la lettre A, juſques au Z.
-|- style="font-family: times, serif; vertical-align:top"
-|O-O or N-N is the ''Perpendicular Diameter''.
-|OO ou NN. Eſt le ''Diametre perpendiculaire''.
-|- style="font-family: times, serif; vertical-align:top"
-|G-S. ''Oblique Diameter'', which goes obliquely across the circle.
-|GS. ''Diametre oblique'', comme allant par le Cercle obliquement.
-|- style="font-family: times, serif; vertical-align:top"
-|C-W or X-D. Interior Collateral.
-|CW ou XD. ''Collaterale interieure''.
-|- style="font-family: times, serif; vertical-align:top"
-|G-T or S-F. ''Exterior Collateral''. These last two lines go two by two from one side to the other, without actually being parallel, but which I found best to call Collaterals.
-|GT ou SF. ''Collaterale exterieure''. Ces deux dernieres lignes vont deux & deux l'une à coſté l'autre, ſans toutefous qu'elles ſoyent paralleles, dont nous avons trouvé bon de les nommer Collaterales.
-|- style="font-family: times, serif; vertical-align:top"
-|N-T or N-F. ''Interior Transverses''.
-|NT ou NF. ''Traverſante interieure''.
-|- style="font-family: times, serif; vertical-align:top"
-|W-S or D-G. ''Exterior Transverses''. These last line also go two by two from one side to the other, in the same way as the preceeding ones, called Collaterals. However because they are different and cross the Principal Diameter (the others remain on each side)  I wished to distinguish from the Collateral lines by calling them Transverses.
-|WS ou DG. ''Traverſante exterieure''. Ces derniers lignes vont auſſi deux & deux l'une à coſté l'autre, en la meſme ſorte que les precedentes, appellées collaterales: toutesfois pource qu'elles en different, en ce qu'elles vont à travers le Diametre principal (les autres demeurants à coſté) nous les avons voulu diſcerner d'avec leſdites Collaterales, par le Nom de Traverſantes.
-|- style="font-family: times, serif; vertical-align:top"
-|A-O-Z-O is the ''Outside Square''.
-|AOZO. Eſt le ''Quarré circonſcrit''.
-|- style="font-family: times, serif; vertical-align:top"
-|A-O. ''Side of the Outside Square''.
-|AO. ''Coſté du Quarré circonſcrit''.
-|- style="font-family: times, serif; vertical-align:top"
-|C-D-F-N, with the Centre, is one ''Quadrant du Cercle''.
-|CDFN avec le Centre, font un ''Quadrant du Cercle''.
-|- style="font-family: times, serif; vertical-align:top"
-|C-N-X-N. The ''Inside Square''.
-|CNXN. Le ''Quarré inſcrit''.
-|- style="font-family: times, serif; vertical-align:top"
-|C-N. ''Side of the Inside Square''.
-|CN. ''Coſté du Quarré inſcrit''.
-|- style="font-family: times, serif; vertical-align:top"
-|A-B-C-B. ''Quadrangle''. So that the name ‘Square’ is not overused and would consequently lead to confusion by the reader, we have found it best to refer to these small Squares as Quadrangles.
-|ABCB. ''Quadrangle''. Afin que ce nom de Quarré ne ſuiſt trop frequent, & conſequemment, ſujet à troubler la conſideration du Lećteur, nous avons trouvé bon, de nommer ces petits Quarrez, Quadrangles.
-|- style="font-family: times, serif; vertical-align:top"
-|C-A. ''Extended Diameter''.
-|CA. ''Diametre prolongé''.
-|- style="font-family: times, serif; vertical-align:top"
-|B-B. the ''Diagonal'' of the Quadrangle.
-|BB. La ''Diagonale'' du Quadrangle.
-|- style="font-family: times, serif; vertical-align:top"
-|The little line that goes between the aforesaid Diagonal & the exterior angle across the Extended Diameter, shall be called the ''Foot-Line'' or ''Pedal Line'', because it is exactly the length of the foot.
-|Ceſt petite ligne qui va entre ladite Diagonale & l'angle exterieur, croiſant le Diametre prolongé, ſera nommée ''ligne du Pied'', ou ''ligne Pedale'', pour ce qu'elle egale juſtement la longueur de la plante.
-|- style="font-family: times, serif; vertical-align:top"
-|The figures which take up three-quarters of the Quadrangles and which extend in a parallelgram along the each of the edges of outside square to the meet the circumference are called the ''Square Extension'', and consequently the line, drawn from the end of the Foot-Line through the centre of the Quadrangle to the edge of the Circumference is called the ''Length of the Square Extension'': the other running from the circumference to the edge of the Outside Square is called the ''Width of the Square Extension''.
-|La figure qui comprend au dedans de chaſcun des Quadrangles les trois quarts, avec deux egaux parallelogrammes au dehors, l'un à l'un des coſtez, & l'autre à l'autre, allants juſques à la circonference, ſera nommée ''l'Eſquierre'', & conſequemment la ligne, tirée depuis le bout de la ligne Pedale par le centre & le coſté du Quadrangle juſques à la circonference du Cercle, ſera dite la ''longeur de l'Eſquierre'': l'autre allant depuis le coſté du Quarré circonſcrit juſques à la meſme circonference la ''largeur de l'Eſquierre''.
-|- style="font-family: times, serif; vertical-align:top"
-|These are the names of all the lines which we will use in practice: of course those lines not expressly specified in this list by their letters will have the same names as the opposite and similar lines or figures. Also note that the names are for the entire line, from one end to the other, we have referred to letters not for measurement, but only to show where they go.
-|Voilà les noms de toutes les lignes, qui ont de l'uſage en la Pratique: bien entendu que celles qui ſe ſont pas expreſſement ſpecifiées en ce denombrement par leurs lettres, auront les meſmes appellations que les lignes ou figures oppoſites, & ſemblables. Et faut ſçavoir, que leſdites appellations leur ſont attribuées en leur entier, depuis l'un bout juſqu'à l'autre; car nous ne mettons pas les lettres pour meſurer, mais ſeulement pour montrer les lignes.
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
-|'''Circle No 1'''
-|'''Cercle N.1.'''
-|- style="font-family: times, serif; vertical-align:top; font-style: italic"
-|Representation and relation of the proportions of the body & limbs of Man to the figure of our circle.
-|Repreſentant & rapportant les proportions du Corps & des Membres exterieurs de l’Homme à la figure de noſtre cercle.
-|- style="font-family: times, serif; vertical-align:top"
-|We begin now to measure the proportions of Man, and relate them to this circle where they will be perchance be perceived with far more appreciation than we had above, when the proportions were found by chance. The reason for such admiration is that lines drawn between angles opposite to each other, themselves derived from no other reference than just the length of the Radius, accord so exactly with so many proportions of the body, as presented in this Circle No 1. It is  not merely observation and practice that demonstrates this truth is as amazing as it is useful. It shall be made manifest to all those, who would take pains to examine the demonstrations which shall be proposed following this same explanation. Into which we shall enter through the description of Circle No 1, which represents all the proportions of Man, from the front, and therein is the significance which follows.
-|Nous commencerons maintenant à meſurer les proportions de l’Homme, en les rapportant à la figure de ce Cercle, où elles ſeront recogneuës paradventure avec plus d’admiration qu’elles ont eſté trouvées deſſus avec hazard. Car quelle raiſon, que les lignes d’une figure tirées des angles oppoſites les uns aux autres (ſans nulle adreſſe, que de la ſeule longeur de demi-Diametre) ſe puiſſent accorder ſi juſtement avec tant de proportions, comme il eſt repreſenté ſur ce Cercle N.1. ſinon la ſeule obſervation & l’experience, qui en demonſtre la verité auſſi admirable, que l’utilité en eſt grande; comme il ſera manifeſte à touts ceux, qui voudront prendre la peine d’en examiner les demonſtrations, qui ſeront propoſées à la ſuite de ceſte meſme explication. A laquelle nous ferons l’entrée par la declaration du Cercle N.1. repreſentent les proportions de l’homme, à le regarder de front; & en eſt la ſignification telle qu’il s’enſuit
-|- style="font-family: times, serif; vertical-align:top"
-|C-X: The entire Diameter is equal the the extended height of the hand raised directly overhead.
-|CX. Le Diametre entier eſt egal à ſa hauteur eſtendue, en eſlevant les bras droitement en haut.
-|- style="font-family: times, serif; vertical-align:top"
-|V: From C to V, is exactly the length of a person, from the soles of the feet to the top of the head.
-|V. Depuis le C. juſques à l’V, c’eſt juſtement la longeur de la personne, depuis les plantes des pieds juſqu’au plus haut de la teſte.
-|- style="font-family: times, serif; vertical-align:top"
-|A: This first dotted line, labelled with a small-A, shows the height of the forehead.
-|A. Ceſte permiere ligne poinćtée, qui eſt marqée à coſté d’un petit A, demonſtre la hauteur du front.
-|- style="font-family: times, serif; vertical-align:top"
-|B: The line B, taken across the Principal Diameter from one S to the other, is exactly at the tip of the nose.
-|B. La ligne B, menée à travers le Diametre principal, de l’un S, à l’autre, reſpond juſtement ſur le bout du nez.
-|- style="font-family: times, serif; vertical-align:top"
-|C: This line shows the chin
-|C. Ceſte-cy demonſtre le menton.
-|- style="font-family: times, serif; vertical-align:top"
-|D: The larynx.
-|D. Le noeud de la gorge.
-|- style="font-family: times, serif; vertical-align:top"
-|E: The height of the shoulders.
-|E. Le haut des eſpaules.
-|- style="font-family: times, serif; vertical-align:top"
-|R: This is the top of the chest.
-|R. Ceſt le plus haut de la poitrine.
-|- style="font-family: times, serif; vertical-align:top"
-|F: The exact height of the armpits.
-|F. Reſpond ſur la juſte hauteur des aixelles.
-|- style="font-family: times, serif; vertical-align:top"
-|G: On the breast (pectorals).
-|G. Sur les mammelles.
-|- style="font-family: times, serif; vertical-align:top"
-|H: On the middle of the chest.
-|H. Sur le mitan de la poitrine.
-|- style="font-family: times, serif; vertical-align:top"
-|I: On the tip of the breastbone.
-|I. Sur le brechet.
-|- style="font-family: times, serif; vertical-align:top"
-|K: On the floating ribs & the diaphragm.
-|K. Sure les fauſſe coſtes, & ſur le Diaphragme.
-|- style="font-family: times, serif; vertical-align:top"
-|The centre is on the navel.
-|Le Centre vient ſur le nombril.
-|- style="font-family: times, serif; vertical-align:top"
-|L: On the head of the thigh-bone.
-|L. Sur la teſte de l’os de la cuiſſe.
-|- style="font-family: times, serif; vertical-align:top"
-|M: On the peritoneum.
-|M. Sur le perinee.
-|- style="font-family: times, serif; vertical-align:top"
-|N: On the virile member.
-|N. Sur le membre viril.
-|- style="font-family: times, serif; vertical-align:top"
-|O: On the thumb.
-|O. Sur le podex.
-|- style="font-family: times, serif; vertical-align:top"
-|P: On the top of the thigh.
-|P. Sur le haut de la cuiſſe.
-|- style="font-family: times, serif; vertical-align:top"
-|H: The thickest part of the thigh.
-|H: Reſpond au plus gros de la cuiſſe.
-|- style="font-family: times, serif; vertical-align:top"
-|Q: shows the concavity of the same.
-|Q. Demonſre le concave de la meſme.
-|- style="font-family: times, serif; vertical-align:top"
-|R: The bottom of the thigh
-|R. Le bas de la cuiſſe.
-|- style="font-family: times, serif; vertical-align:top"
-|S: The top of the kneecap.
-|S. Le ſur-genouil.
-|- style="font-family: times, serif; vertical-align:top"
-|T. The bottom of the kneecap.
-|T. Le ſous-genoil.
-|- style="font-family: times, serif; vertical-align:top"
-|E: This is the highest point on the shin.
-|E. C’eſt le plus haut de la greve.
-|- style="font-family: times, serif; vertical-align:top"
-|V: The inside top of the calf.
-|V. Le haut de gras de la jambe en dedans.
-|- style="font-family: times, serif; vertical-align:top"
-|W: The same on the outside.
-* He has V & W backwards
-|W. Le meſme en dehors.
-|- style="font-family: times, serif; vertical-align:top"
-|X: The lowest part of the calf on the inside.
-|X. Le plus bas du meſme en dedans.
-|- style="font-family: times, serif; vertical-align:top"
-|Y: The bottom of the shin.
-|Y. Le bas de la greve.
-|- style="font-family: times, serif; vertical-align:top"
-|Z: The ankle.
-|Z. La cheville du pied.
-|- style="font-family: times, serif; vertical-align:top"
-|C: the soles.
-|C. Les Plantes.
-|- style="font-family: times, serif; vertical-align:top"
-|Anyone interested in reducing these same proportions to some particular measure, to better understand the rationale, could divide the Diameter into 24 Spans, & subdivide each of these into 10 parts, & each part into 10 minutes. Thus it will be the same with stick or with cord, with which one would measure a person. And thus he will find, by the comparison with this figure, the lengths and widths of each of his limbs, which any could easily check. What is more, these measures always match, each one to its own line, parts of lines, which we see in this same Circle.
-|Qui ſera cuirieux de reduire ces meſmes proportions à quelque certaine meſure, pour en ſçavoir rendre la raiſon plus exaćtemēt, il pourra pour ceſt effect partir le Diametre entier en 24. Nombres, & à chaſcun d’iceux il y pourra imaginer 10. parcelles; & à chaſcune parcelle 10. minutes: dont il fera pareillement le ſemblable du baſton ou de la cordelle, dequoy il prendra les meſures au corps de la perſonne. Et par ainſi il trouvera par la confrontation de ceſte figure, raportée à l’experience meſme, à combien montront les longeurs & largeurs de chaſcun des membres, deſquels il voudra faire preuve. Et qui plus eſt, il les trouvera touſiours accordantes en leurdite meſure, à l’une ou à l’autre ligne, ou à certaines parties de lignes, qu’on voit en ce meſme Cercle.
-|- style="font-family: times, serif; vertical-align:top"
-|As the size of the head from the from the top to the chin matches the length of the Foot-Line, or to the half-diagonal of the Quadrangle, therefore it equals the length of the sole of the foot.
-|Car la longeur de la teſte depuis le ſommet jusſques au menton, s’accord juſtement à la meſure de la ligne Pedale, ou à la demie Diagonale de Quadrangle, eſtant par conſequent egale à la meſure de la plante des Pieds.
-|- style="font-family: times, serif; vertical-align:top"
-|Its width is equal to the half-side of the Quadrangle, which is also equal to the length of the hand, from the wrist to the fingertips.
-|Sa largeur eſt egal au demi-coſté du meſme, qui eſt auſſi egale à la longeur de la main, depuis le poignet jusſques aux bouts des doights.
-|- style="font-family: times, serif; vertical-align:top"
-|The length of the arm, with the hand, is equal to one third the Diameter, that is, from the letter R to the letter H, or from H to C, as the lengths are equal, and contain precisely the extension of 8 Spans, since there are 12 on the radius, or on the blade of our sword, as shall be discussed later.
-|La longeur du bras enſemble avec la main, eſt egale à la troiſieme partie du Diametre entier, aſſavoire depuis la lettre R, juſques à l’H. ou depuis ledit H, juſques au C. car ces longeurs ſont egales; & contiennet juſtement l’eſtendue de 8. Nombres, tels qu’il y en 12 ſur le demi-Diametre, ou ſur la lame de noſtre eſpee, commeil ſera diſcouru cy apres.
-|- style="font-family: times, serif; vertical-align:top"
-|All these proportions that are found so amazingly well on these lines, which cut across this figure from one angle to the other, are here shown, in this No 1 Circle on the front of the figure, on the fleshed side as on the skeletal side, because these are the principle basis of the lengths, widths, and all dimensions of Man which is necessary to show on both sides, on the right hand side and the left hand side. The same proportions are shown as well on the profile of the skeleton in Circle No 3. And in No 4, on the backside, showing the person from behind. Again, it is shown in Circle No 5 by the inverted figure, that these same proportions remain invariable whether one begins at one end of the Diameter or the other.
-|Toutes ces proportions ſe rencontrants ſi merveilleuſement ſur ces lignes, qui procedent des entrecoupures de ceſte figure, de l’un des angles oppoſites à l’autre, ſont icy repreſentées en ce Cercle N. 1. ſur le devant de la perſonne, tand ſur la chair, que ſur les oſſements nuds, à raiſon qu’iceux ſont le principal fondement des longeurs, des largeurs,  de toutes les dimenſions de l’homme: dont it nous a ſemblé neceſſaire de le repreſenter en toutes les deux manieres, l’une à main droite, & l’autre à gauche. Les meſmes proportions ſont demonſrées areillement ſur le poufil des oſſements au Cercle N.3. Et au N.4. ſur le derriere, en regardant la perſonne de dos. Comme il eſt derechef repreſenté au Cercel N.5. par la figure renverſée, que ces meſmes proportions demeurent invariables tant à commencer de l’un bout du Diametre, que de l’autre.
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
-|'''Circle No 2'''
-|'''Cercle N. 2.'''
-|- style="font-family: times, serif; vertical-align:top"
-|This circle contains only the names of the lines of this figure, as detailed above.
-|Ce Cercle ne contient autre choſe, que les noms des lignes de ceſte figure, en la meſme ſorte qu’ils on eſté declarez cy deſſus.
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
-|'''Circle No 3'''
-|'''Cercle N.3.'''
-|- style="font-family: times, serif; vertical-align:top"
-|''In which one sees how the natural pace which men ordinarily use as they walk, reliably matches with the measurements of this same Circle.''
-|''Auquel on voit, comment les pas naturels, dont les Hommes uſent en leur demarche ordinaire, s’accordent fort raiſuement avec de meſures de ce meſme Cercle.''
-|- style="font-family: times, serif; vertical-align:top"
-|Thus as we have shown how this Circle comes from the proportions of Man, we also do the same with regard to the steps and paces he shall use in our Training. Insofar as the proportions are again represented in Circle No 3 on the skeleton profile, there is no point to say anything other than to refer the reader to what has already been explained about Circle No 1.
-Note: The text of the square in the centre reads:
-"Gerardus Thibault Inventor"
-|Ainſi que nous venons de representer la convenance de ceſt figure du Cercle avec les proportions de l’Homme faiſons en auſſi le ſemblable au regard de la demarche & des pas, deſquels il qu’il uſe en ceſtuy noſtre Exercice. Car touchant ce que les proportions de l’homme font derechef repreſentées en ce Cercle N.3. ſur le pourfil des oſſements, il n’en eſchet point de propoſer icy autre choſe, que d’en renvoiyer ſimplement le Lećteur à ce qui a eſté ſpecifié au Cercle N.1.
-|- style="font-family: times, serif; vertical-align:top"
-|The footprints, which go in and about Circle No 3, marked with different numbers, demonstrate the concordance between the ordinary walking pace of a man and the Circle. Their significance is as follows.
-|Les traces donc les pieds, qui vont dedans & alentour de ce Cercle N.3. cottés en chifre de differents nombres, demonſtrent la convenance de la demarche ordinaire de l’homme avec ceſte meſme figure du Cercle, & en eſt la ſignification telle, que s’enſuit.
-|- style="font-family: times, serif; vertical-align:top"
-|Those which go along the Perpendicular Diameter, marked number 1, demonstrate that the length of this Extended Diameter equals four ordinary paces, in doing three or four paces before coming into the circle, for balance, begin stepping with the right foot on the Foot-Line and end likewise on the opposite Foot-Line with the left foot. Which one can also observe similarly in the other paces which follow.
-|Celles qui vont le long du Diametre perpendiculaire, cottées en chifre 1, demonſtrent que la longeur de cedit Diametre perpendiculaire prolongé, revient à quatre pas ordinaire, en faiſant deux ou trois pas avant que de venir au Cercle, afin que le corps ſoit en train, pour commencer la demarche à main droite ſur la ligne Pedale, & a finir pareillement ſur la ligne Pedale à main gauche. Ce qui doit auſſi eſtre obſervé ſemblablement és autres  demarches ſuivantes.
-|- style="font-family: times, serif; vertical-align:top"
-|Those which go along the same Diameter within the circumference, marked number 2, demonstrate that three normal paces is the length of this Diameter from circumference to circumference.
-|Celles qui vont le long du meſme Diametre au dedans de la circonference, marquées en chifre 2, demonſtrent qu la longeur de ce Diametre eſt de trois pas de la demarche ordinaire, en allant de circonference à circonference.
-|- style="font-family: times, serif; vertical-align:top"
-|The same proportion is shown on the two Oblique Diameters by the footprints numbered 3 & 4 as well as those which are marked number 5 on the four sides of the Outside Square, which are equal to those along the Oblique Diameters, which go from one edge to the other.
-|La meſme proportion eſt repreſenté ſur les deux Diametres obliques par les ſemelles, qui portent le Nombre 3. & 4. & pareillment par celles qui portent le Nombre 5. ſur les quatre coſtez du Quarré circonſcrit, comme eſtants egaux à iceux Diametres obliques, en allant touſiours de l’un bout juſqu’a l’autre.
-|- style="font-family: times, serif; vertical-align:top"
-|Those marked with number 6 demonstrate how the circumference, along with the Inside Square, matches eight steps at an ordinary pace, which can be done by putting the left foot along the circumference line at C, then moving the other forward and place it at G, in the middle of the line. Then drawing the left circularly along circumference from C to N. Then again advancing the right along the same side of the Inside Square close to the left & then continuing to follow along the next side of the Inside Square to S, and so on, so the right foot always follows the four lines of the Inside Square, and the left is carried around always following the circumference. The right foot reaches two half-sides of the Inside Square with each step, and the left moves a Quadrant of the circumference each time.
-|Celles qui ſont marquées du Nombre 6. demonſtrent la convenance de la Circonference, enſemble avec le Quarré Inscrit, à la demarche de huićt pas ordinaires: leſquels on y pourra pratiquer en mettant premierement le pied gauche ſur la lettre C. & cheminant de l’autre en avant juſques à le planter à plein, ſur le G. au milieu de la ligne; menant apres le gauche circulairement le long de la circonference depuis C juſques à N: puis avançant derechef le droit le long du meſme coſté du Quarré inscrit jusſques à bien pres de l’autre, & continuant à le porter par la trace d l’autre prochain coſté du Quarré inſcrit juſques à l’S. & ainſi conſequemment du reſte, en ſorte que le pied droit aille touſiours ſuivant les quatres lignes du Quarré Inſcrit, & le gauche ſoit porté en rond coſtoyant touſiours la circonference; le pied droit achevant à chaſque demarche deux moitiez de deux coſtez du Quarré inſcrit, & la gauche achevant à chaſque fois un Quadrant du circonference.
-|- style="font-family: times, serif; vertical-align:top"
-|One should always be very aware of this concordance, in as much as this, the length of a man’s ordinary walking pace, is our exemplar. So our imitation of which always informs the style of our School. This shall be shown throughout the rest of this book and by which means we avoid awkward and inconvenient poses, which we shall see when and where an example requires a more precise explanation.
-|L’obſervation de ceſte convenance doit eſtre tenue en grande eſtime, d’autant que ce ſont là les pas ordinaires de la demarche de l’homme, à l’exemple & imitation de laquelle nous devons touſiours former le ſtile de noſtre Pratique, ainſi qu’il paroiſtra par la ſuite de tout le livre, & que ſans iceux il ne ſeroit poſſible d’eviter des grandes incommoditez, qui ſeront données à cognoiſtre, où il ſera queſtion d’en rendre la raiſon plus exaćte.
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
-|'''Circle No 4'''
-|'''Cercle N.4.'''
-|- style="font-family: times, serif; vertical-align:top"
-|''Which Contains the explanation of the Range of the three Approaches, or Instances, & how they are represented on our Circle, both along the Diameter, and on the sides of the Inside Square, to close with the Enemy from the side.''
-|''Contenant la declaration de la Meſure des trois Approches, ou Inſtances, & comment elles ſont repreſentées ſur noſtre Cercle, tant ſur le Diametre, que ſur les coſtez du Quarrée Inſcrit, pour aborder l’Ennemi de travers.''
-|- style="font-family: times, serif; vertical-align:top"
-|First, is shown here the proportions of Man as seen from the back.
-|Pour le premier on vous repreſente icy les proportions de l’Homme, à le regarder de dos.
-|- style="font-family: times, serif; vertical-align:top"
-|Second, from the footprints, to the right and left of the figure, demonstrate the concordance of paces which was observed in the previous Circle.
-|Secondement par les traces des ſemelles, à droite & à gauche de lafigure, on y pourroit demonſtrer la meſme convenance des pas, qui a eſté remarquée au Cercle precedent.
-|- style="font-family: times, serif; vertical-align:top"
-|To understand this, one must know that the two adversaries will first close with each other at the First Instance, that is, when one, in the Z-X Quadrangle, places his right foot on the extended side and the left foot on the Foot-line, the other does the same in the A-C Quadrangle, opposite, as is clearly shown by the footprints marked on them. While they are at this range, we say they are at the First Instance, for if they were further away, they would be out of range, because they would be unable to hit each other even in the slowest time because they would be almost completely beyond their reach.
-|Pour l’intelligence deſquelles il faut ſçavoir, que les deux Contraires ſe viennent premierement aborder à la Premiere Inſtance. c’eſt à dire, quand l’un ſe vient placer ſur le Quadrangle ZX, le pied droit ſur le coſté exterieur, & pied gauche ſur la ligne Pedale; que l’autre ſe vient pareillement placer alencontre ſur le Quadrangle oppoſite AC; comme il eſt clairement repreſenté par les traces des pieds, qui ſont marquez deſſus. Tandis qu’ils ſont en ceſte meſure nous diſons qu’ils ſont à la Premiere Inſtance; car s’ils ſe tiennent plus loing, ils ſont comme hors de meſure, à cauſe qu’ils ne ſe peuvent toucher l’un l’autre en temps mediocre, par ce qu’ils ſont quaſi hors de leur portée.
-|- style="font-family: times, serif; vertical-align:top"
-|The Second Instance is that which comes so close to the adversary, either directly by the path of the Diameter, or in approaching from the side by the Quadrants, that one can put the point of the sword on the elbow, and, consequently, hit him in half-time with a simple bow of the body with the feet firmly planted. Which one can do by moving along the diameter to the letter E, and on the G by the sides of the Inside Square. This range is called the Second Instance, because one cannot approach that close as the point of first contact without first having previously secured one’s line of approach. And once there, one works from a superior postion, because it merely requires a simple extension of the arm, assisted by a simple bow of the body, which has no effect on one’s balance, to hit the enemy.
-|La Seconde Inſtance eſt celle qui vient ſi pres de la partie adverſe, ſoit en allant droićtement ſur luy par la voye du Diametre, ou en l’approchant de travers par les Quadrants, qu’on luy puiſſe mettre la pointe de l’eſpee ſur le coude, & par conſequent on le peut toucher en un demi-temps avec un ſimple panchement du corps & à pied ferme. Ce qu’on pourra faire en arrivant par le Diametre à la lettre E. & ſur le G, par les coſtez du Quarré Inſcrit. Ceſte meſure ſe nomme Seconde Inſtance, pource qu’on n’y peut venir de permier abordee, ſans avoir aſſeuré preallablement ſes approches: & y eſtant, on travaille avec plus d’avantage, car il ne faut qu’une ſimple extenſion du bras, aſſiſté d’un panchement de corps, qui n’empeſche pas de le retenir en balance, pour toucher l’Ennemy.
-|- style="font-family: times, serif; vertical-align:top"
-|From the Second Instance, we come to the Third, which is at the letter H on the Diameter, or along the sides of the Inside Square at the letter N. It is a range at which one can hit the foe while keeping the body straight and upright, without moving the feet, by doing nothing more than extending the arm.
-|De la Seconde Inſtance on vient à la Troiſieme, qui eſt à la lettre H, ſur le Diametre, ou ſur les coſtez du Quarré Inscrit, à la lettre N. ceſt une meſure en laquelle on peut donner l’atteinte au Contraire, en tenant le corps droit & eſtēdu ſans aucun avancement pieds, ne faiſant rien autre que d’allonger le bras.
-|- style="font-family: times, serif; vertical-align:top"
-|Those are our Three Instances, along the Diameter, as along the sides of the Inside Square, to the right and the left, where they are clearly marked by the footprints, which show the situation as stationary paces, one foot distinguished from the other by a single foot (distance) between the arches of each footprint, as we are used to when standing upright.
-|Et voilà nos Trois Inſtances, tant ſur le Diametre, que ſur les coſtez du Quarré Inſcrit, à droite & à gauche, où elles ſont repreſentées aſſez clairement par les semelles, qui en demonſtrent la ſituation en forme de pas arreſté, l’un pied eſtant diſioinćt de l’autre de l’intervalle d’un pied tant ſeulement, entre le creux de l’un & de l’autre, ainſi qu’on eſt accouſtumé de ſe tenir debout à pieds arreſtez.
-|- style="font-family: times, serif; vertical-align:top"
-|Also, as much as it is a very important point in the practice of arms, to know these three Approches distinctly, as they are represented on the Circle. It is also an important point in Theory to consider how these ranges are taken solely from the proportions of Man. As such it is more and more apparent, that we always take Nature as our guide, and from these proportions, we align our steps, our approaches, and our distances, either when we stay or when we move. Because if you look only at the figure of the man, here shown from the back, you will see that,in the First Instance, the interval from circumference to circumference is equal to the extended height of a person, so that when the two Parties are in this First Instance, there is always this same gap equal to the extended height of a person between them. And if they are at the Second, either straight across the Diameter or to one side along the edges of the Square, the distance between them is equal to the natural height of that same person, from the soles of the feet to the top of the head. And finally, the interval of the Third is equal to the height of the stomach.
-|Or comme c’eſt un poinćt de treſgrande importance en la Pratique des armes, de cognoiſtre ces trois Approches diſtinćtement, comme elles ſont repreſentées par le Cercle: auſſi eſt ce choſe tres digne de conſideration en la Theorie de contempler, comment les meſures en ſont tirées de la ſeule Proportion de l’Homme; afin qu’il apparoiſſe de plus en plus, que nous prenons touſiours la Nature pour guide; & que ſelon les proportions d’icelle, nous dreſſons touts nos pas, nos approches, & nos diſtances, ſoit à demeurer, ſoit à bouger de la place. Car ſi vous regardez tant ſeulement la figure de l’Homme, qui eſt icy representé de dos, vous verrez, que l’intervalle de la Premiere Inſtance de Cironference à Circonference, eſt egale à la hauteur eſtendue de la perſonne, de ſorte que quand les deux Parties ſont en ceſte Premiere Inſtance, il y a touſiours entre deux la meſure de ceſte hauteur eſtendue d’une perſonne. Et s’ils ſont à la Seconde, ſoit de droit ſur le Diametre, ou de travers ſur les coſtez du Quarré ; la diſtance qui eſt entre deux eſt egale à la hauteur & ſtature naturelle du corps de la meſme perſonne, depuis la plante des pieds juſqu’au ſommet de la teſte. Et finalement, l’intervalle de la Troiſieme, eſt egale à la hauteur de la poitrine.
-|- style="font-family: times, serif; vertical-align:top"
-|If I am asked what is the meaning of these fourth pair of footprints at the centre, and if they represent a Fourth Instance on the Diameter, I answer, no, and add that they were added to show how four static paces accord with half the distance of the extended diameter, which is equal to four ordinary steps, which was explained in Circle No 3 & marked number 1. As such, there are but the three pairs of footprints which show the Diametrical Instances, as well as the three others, which go off to the the sides and show the lateral ones.
-|Si on me demande, qu’eſt ce que ſignifie ceſte quatrieme paire de ſemelles, qui attouche le Centre, & ſi elle ne repreſente pas la Quatrieme Inſtance Diametrale, je reſpons, que non; & qu’elle y eſt adjouſtée, pour repreſenter ſimplement la convenance du demi-Diametre prolongé avec quatre pas à pieds arreſtez, comme l’entier eſt egal à quatre pas ordinaires de demarche: ainſi qu’il eſt expliqué au Cercle N. 3. & marqué en ciffre 1. De ſorte qu’il n’y a que les trois premieres paires de semelles, qui demonſtrent les Inſtances Diametrales; ainſi que les trois autres, qui vont aux coſtez, demonſtrent les Laterales.
-|- style="font-family: times, serif; vertical-align:top"
-|Now, everything I have said about these Instances, starting from Quadrangle A-C when the adversary is on Quadrangle Z-X must also be understood to apply conversely, when beginning the approach from the Quadrangle opposite, which is easy to understand from the footprints along the Diameter as well as along the edges of the Inside Square.
-|Or tout ce que nos avons dit de ces Instances, en commenceant par le Quadrangle AC. quand l’Adverſaire ſe tient deſſus le Quadrangle ZX. celà meſme ſe doit auſſi entendre à l’oppoſite, en occaſion, qu’il nous touche de commencer les Approches par le Quadrangle oppoſite ainſi qu’il eſt aiſé à comprendre par les traces des pieds, qui en font la declaration tant ſur le Diametre, que ſur l‘un & l’autre coſté du Quarré Inſcrit.
-|- style="font-family: times, serif; vertical-align:top"
-|To know the exact ranges of each of these three Instances, as well as the basis of several observations, which we shall explore later, one must know that the blades of our swords are differentiated by twelve numbers into equal parts, as shown along the bottom left of the table. The reason for this will be explained following this section. Eight of these parts are the exact length of the arm, which is evident from the figure in Circle No 1, where it clearly shows that length of the arm is equal to one third the Diameter, from R to H: and since the Diameter is two times longer than the blade, that is, twenty-four Spans, it clearly follows that one third equals eight. Also this proof can demonstrate the truth, if one places the tip of the blade at the armpit and extends the arm along the blade, the finger tips only reach as far as the number eight. And therefore, when gripping the sword in hand, the sword has a length of 12, and that of the arm of 8, from which one must subtract about 1 for the shortening of the fingers when one grips, it appears then that holding the sword in hand, one can reach straight ahead a length of 19 Spans. Disregarding other considerations, let us suppose, for a moment, that the two swords are both equal to the radius; there will be more about this later. In this way we can calculate the measurements of these Instances from part 47, book 1 of Euclid in this way.
-|Pour coignoiſtre exaćtement les meſures de chaſcune de ces trois Inſtances, enſemble auſſi le fondement de pluſieurs obſervations, dont il ſera parlé cy apres, il faut ſçavoir, que les lames de nos eſpees ſont diſtinguées par chifres en douze parties egales, comme il eſt repreſenté au bas du Tableau à main gauche, & en ſera la raiſon declarée à la ſuite de ce meſme diſcours. Huićt de ces parties font la juſte longeur du bras, ainſi qu’il eſt evident par la figure du Cercle N.1. où il ſe voit clairement que la longeur du bras eſt egale à un tiers du Diametre, depuis l’R juſques à l’H: & d’autant que le Diametre entier a deux fois autant de longeur que la lame, ce qui monte à vingt & quatre Nombres, s’enſuit neceſſairement que le tiers en ſera comme huićt. Auſſi la preuve en peut demonſtrer la verité; par ce qu’en mettant la poinćt de la lame contre l’aixelle, & eſtendent le bras deſſus, on ne peut atteindre du bout des doigts plus avant que juſqu’au Nombre huićt. Et comme ainſi ſoit, qu’en tenant l’eſpee au poing, on aye la longeur de la lame, comme 12,  & celle du bras comme 8: deſquels il en faut ſoubſtraire quaſi 1 pour le raccourciſſement des doigts, qui font le poing, il paroiſt donc qu’en tenant l’eſpee au poing, on peut atteindre en droite ligne ſi avant que la longeur de 19 de ces meſmes Nombres. Faut d’avantage preſuppoſer pour le ſecōd, que les eſpees ſont egales au demi-Diametre; comme vous entendrez plus particulierement cy apres. Et voilà par où lon pourra calculer les meſures de ceſdites Inſtances par la 47. Liv.1. Eucl. en ceſte maniere.
-|- style="font-family: times, serif; vertical-align:top"
-|The radius from X to the Centre is  <font style="text-align: right"> 12</font>
-|Le demi-Diametre depuis X juſqu’au Centre, eſt <font style="text-align: right"> 12</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Likewise the perpedicular radius,  <font style="text-align: right"> 12</font>
-|Pareillement le demi-Diametre perpendiculaire,  <font style="text-align: right"> 12</font>
-|- style="font-family: times, serif; vertical-align:top"
-|The Centre is a right-angle.
-|L’angle de Centre eſt droit.
-|- style="font-family: times, serif; vertical-align:top"
-|Therefore the line subtended from X to N is approx.  <font style="text-align: right">16.97</font>
-|Doncques la ligne X N, qui le ſouſtient, <font style="text-align: right">16,97@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|That is the line which measures the Third Instance, going by the quadrants of the Circle.
-|Voilà la ligne qui meſure la Troiſieme Inſtance, en allant par les quadrants de Cercle.
-|- style="font-family: times, serif; vertical-align:top"
-|The range of the Second is found in the same way. To do this, first imagine a line perpendicular to the Diametre from G to G. This will cut the radius at a right angle, in the exact middle between C and the Centre. Let’s say, then:
-|La meſure de la Seconde ſe trouve en la meſme ſorte. Et pour ce faire imaginez permierement une ligne allant perpendiculairement par le Diametre, de G à G. Icelle coupera le demi-Diametre en angle droit, au juſte mitan entre le C et le Centre. Dites donc
-|- style="font-family: times, serif; vertical-align:top"
-|The radius is 12, and half of the other radius 6, added together, so the line that goes from X to the right angle is  <font style="text-align: right">18</font>
-|Le demi-Diametre 12 & la moitié  de l’autre demi-Diametre 6, ſont enſemble, pour la ligne qui va depuis l’X juſques à l’angle droit  <font style="text-align: right">18</font>
-|- style="font-family: times, serif; vertical-align:top"
-|The imaginary line being equal to the radius, half of that from the right angle to G must necessarily be  <font style="text-align: right">6</font>
-|La ligne imaginée eſtant egale au demi-Diametre, faut neceſſairement, que la moitié, depuis l’angle droit juſques au G, en ſoit  <font style="text-align: right">6</font>
-|- style="font-family: times, serif; vertical-align:top"
-|The angle at the Diameter is a right angle.
-|L’angle qui touche le Diametre eſt droit.
-|- style="font-family: times, serif; vertical-align:top"
-|Therefore the line subtended from X to G, is about <font style="text-align: right">18.97</font>
-|Doncques la ligne X G, qui le ſoutient, <font style="text-align: right">18,97@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|The range of the First Instance appears by itself, being two times the radius, which makes <font style="text-align: right">24</font>
-|La meſure de la Permier Inſtance paroiſt d’elle meſme, eſtant deux fois le demi-Diametre: qui font par enſemble <font style="text-align: right">24</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Next, then, the arm, extended straight with the sword, makes a length of 19 Spans. The distance of the First Instance is only 24 so one might conclude that from there, one can hit the adversary from the First Instance, by moving only 5 Spans forward, but this is false, which we can physically demonstrate. When two adversaries stand in the opposite Quadrangles, with swords and arms extended in a straight line the tips of the blades will only reach to just before the other’s hilts, as is shown in Circle No 1 of Plate IV: as such that they cannot reach the other’s body without advancing at least as far as the length of their adversary’s arm, that is 7 or 8 Spans.
-|Puis donc que le bras avec l’eſpee font enſemble en droite ligne la longeur de 19 Nombres; & que l’eſpace de la Premiere Inſtance n’en contient que 24, paradventure quelqu’un voudra conclurre de là, qu’on puiſſe toucher ſa partie adverſe depuis la Permiere Inſtance, in avançant ſeluement la meſure de 5 Nombres; ce qui eſt faux, comme on le peut demonſtrer par experience. car quand les deux parties adverſes ſe tiennent ſur les Quadrangles oppoſites en la forme requiſe, avec les bras & eſpees eſtendus en droite ligne les poinćtes des lames n’arriveront chaſqu une, que juſques au devant de la garde contraire: ainſi qu’il eſt repreſenté ſur le Cercle N.1. du Tableau IV: de ſorte qu’ils ne peuvent arriver au corps contraire ſi ce n’eſt qu’ils s’avancent pour le moins, autant que tout le bras entier de leur partie adverſe, qui eſt de 7. à 8. Nombres.
-|- style="font-family: times, serif; vertical-align:top"
-|The reason for this is when the body is held erect on both feet, with one foot on the edge of the Quadrangle and the other on the Foot-Line, one does not balance over the ball of the right foot at the Circumference, but rather between the two feet over the centre of the Quadrangle. Having considered and looked at the placement of the feet, which are separated by about a foot, on can conclude with assurance that each of the adversaries is half-foot back. And from this comes the increase in distance of the First Instance.
-|La cauſe en eſt, que le corps, ſe tenant ainſi debout ſur ſes pieds, placez l’un ſur l’un des coſtez du Quadrangle, & l’autre ſur la ligne Pedale, ne repoſe pas ſur la poinćte du pied droićt qui aboutit à la Circonference; mais il revient entre les deux pieds par deſſus le Centre du Quadrangle. Ce qu’eſtant bien conſideré, & confronté à la ſituation deſdits pieds, qui ſont ſeparez entre eux d’un pied entier d’intervalle; on pourra conclurre aſſurement, que chaſcun des Contraires ſe recule d’un demi-pied en arriere. Et voilà d’où procede l’aggrandiſſement de la Permiere Inſtance.
-|- style="font-family: times, serif; vertical-align:top"
-|As to the range of the Second, it must be expanded likewise, adding the slight withdrawal of the two bodies, following the placement of the feet, which together comes to one extra foot length between the two. Therefore it follows that, as much as the Collateral X-G only goes to about 18.97 Spans, we must always count the distance as about 21, 45, which is just about 21 ½.  As such one cannot hit the adversary without advancing by one foot distance, which can be reached by simply leaning forwards with the torso.
-|Quant à la meſure de la Seconde, il la faut aggrandir pareillement, en y adjouſtant le reculement des deux corps, procedant de la ſituation de leurs pieds, qui revient auſſi à un pied de longeur pour touts les deux ensemble. Suivant quoy, combien que la ligne Collaterale X G ne monte qu’à 18,97@ Nombres; toutesfois il en faut conter pour la diſtance 21,45@ qui eſt à bien peu pres 21½. En ſorte qu’on n’y peut toucher la partie adverſe, ſinon qu’on s’avance environ la meſure d’un pied, laquelle on peut atteindre en panchent ſeulement du corps ſur le devant.
-|- style="font-family: times, serif; vertical-align:top"
-|The line of the Third Instance X-N was calculated at about 16.97 Spans, to which we again add the distance of one foot to adjust for the stance, which comes to a about 19.45 Spans, just a little less than 19 ½. So, as the extension of the arm with the sword comes to 19 Spans, that leaves about ½ Span to hit. Thus it is easy to understand how, in this Third Instance, one can hit an adversary while standing erect, with only the slightest bow.
-|La ligne de la Troiſieme Inſtance X N a eſté calculée 16,97@. à laquelle adjouſtant derechef la meſure d’un pied en recompenſe de la ſituation; il en vient Nombres 19,45@ qui font un peu moins que 19½ . De ſorte que, l’extenſion du bras avec l’eſpee faiſant enſemble 19, il en reſte environ ½ Nombre de meſure pour atteindre. Dont il eſt aiſé à comprendre, qu’à ceſte Troiſieme Inſtance on peut toucher ſa partie adverſe, en ſe tenant droit, avec le moindre panchement du monde.
-|- style="font-family: times, serif; vertical-align:top"
-|Then, because we have explained the ranges of the Lateral Instances, it makes sense to to the same with the others. And this, furthermore, because of the differences which are found between the two, could perhaps give reason to someone to suspect some fault, as if the Instances on the Diameter were not properly aligned.
-|Or puis que nous avons declaré les meſures des Inſtances Laterales, il eſt raiſon de faire auſſi le ſemblable des autres. Et ce d’autant plus, parce que la difference, qui ſe trouve entre deux, pourra donner paraventure occaſion à quelqu’un d’y ſoupçonner quelque faute, comme ſi les Inſtances Diametrales n’eſtoyent pas bien aſſignées.
-|- style="font-family: times, serif; vertical-align:top"
-|In fact the line X-H, which represents the Third Instance interval, is shorter than the line X-N. Because that one was calculated to be about 16.97 Spans & this one is no more than 16.  This is easy to show by the rule of Proportion: imagine again the triangle, which was described above for the calculation of the line X-G. Let’s say the length from X to the middle of the cross radius is 18, for the base, which gives 6 for the height to G. Therefore the base from X to the centre being 12, the height from this Centre to the letter L will be 4. So it is that the lines from the Centre to L & to H are equal by proposition 4 of Euclid’s 1st  book. These 4, added to the radius 12, for the line X-H comes to 16. Thus this line of the Third Instance on the Diameter comes to only 16 Spans, and the other about 16.97. In any case the difference is made up in another way as we shall soon see. Similarly there is a difference between the lines X-G & X-E for the Second Instance: as the first is about 18.97 Spans, and the other about 19.69, calculation of which we shall leave for the present as this would involve too many sums, you may, meanwhile find this by means of the two triangles G-C w.
-|Et de fait la ligne X H, qui y repreſente l’intervalle de la Troiſieme Inſtance, eſt plus courte que n’a eſté la ligne X N. Car ceſte-là a eſté calculée à Nombres 16,97@: & celle-cy n’en contient que 16. ſans plus. Ce qui eſt aiſé à demonſtrer par le regle de Proportion: imaginant derechef le triangle, qui a eſté declaré cy deſſus pour la calculation de la ligne X G. Diſons, la longeur depuis X juſques au milieu de l’autre demi-Diametre 18, pour la baſe; donnent 6, pour la hauteur juſques à G. Doncques la baſe depuis X juſques au Centre eſtant 12; la hauterur depuis ledit Centre juſques à la lettre L, fera 4. Or eſt il que les lignes depuis le Centre juſqu’à L, & juſqu’à H, ſont egales par la prop.4. liv.1. d’Euclid. Iceux 4. adjouſtez au demi-Diametre 12; il en vient pour la ligne X H, 16. Ainſi donc ceſte ligne de la Troiſieme Inſtance Diametrale ne fait que 16 Nombres; & l’autre, 16,97@. Toutesfois la difference en eſt recompenſée par une autre voye, comme il ſera declaré tantoſt. Semblablement il y a de la difference entre les lignes X G & X E. pour la Seconde Inſtance: car la permiere eſt de 18,97@ Nombres, & l’autre de 19,69@ ce que nous laiſſerons pour le preſent de calculer, à cauſe que le choſe requerroit trop de ſommes; vous advertiſſant cependent, qu’on en trouvera l’iſſue par les deux triangles G C w.
-|- style="font-family: times, serif; vertical-align:top"
-|In order to reconcile the reason for this difference, you must understand that the usual means of approaching an adversary in our Training is to always move a bit to the side, that will be described elsewhere, to avoid motion directly along the Diameter, which is very hazardous. Thus it is more necessary to understand the distances of these Instances, which approach from the side, than those which go directly towards the Enemy along the Diameter. In any case, the fact of these differences, which appear in the relative distances between the Second and Third Instances, are, practically, of little import, because the inequality between the two lines in the Second Instance is compensated for in the different positions of the body. For one who approaches, coming to the Lateral Second Instance, turns on the heels, in such a way as to move the body backwards about a half-foot; and in the Diametrical Second Instance, will have his heels further forward and his body in profile, so that the slight interval between these two Instances is equalized by the position of the body. As to the difference between the two Third Instance lines X-N & X-H, this is equalized because when one strikes from the Lateral Third Instance, one leans forward. Thus the range is shortened by as much as the line appears to be longer.
-|Pour accorder le different, ſachez que c’eſt l’ordinaire de noſtre Exerice d’aborder le Contraire, en allant touſiours un peu à coſté, pour eviter la trace du Diametre, qui eſt plen de hazard, pour les conſiderations, qui ſeront delcarées autrepart. Dont nous eſtimons, qu’il eſt plus neceſſaire de cognoiſtre les meſures des Inſtances, qui vont en traverſe, que celles qui vont tout droitement ſur l’Ennemi par la voye du Diametre. Toutesfois qu’à la verité la difference, qui ſemble eſtre entre ces meſures des Inſtances Secondes & Troiſiemes, ne donne point de difference en la Pratique, puis que l’inegalité, qui eſt entre les deux lignes des Inſtances Secondes, ſe recompenſe par la diverſe ſituation du corps. Car celuy qui fait les approches, venant à la Seconde Inſtance Laterale, ſe deſtourne avec les talons, en ſorte qu’il ſe recule le corps d’un demi pied de longeur en arriere: & eſtant à la Seconde Inſtance Diametrale, il tient les talons plus avancez, & le corps tout en pourfil: de ſorte que l’intervalle de ces deux Inſtances en eſt egalée par la diverſe ſituation de ſon corps. Et quant à la difference, qui eſt entre les deux lignes des Inſtances Troiſiemes, aſſafoir X N, & X H: elles ſont egalées par ce que quand on donne  l’atteinte à la Troiſieme Inſtance Laterale, cela ſe fait avec le corps panché en avant. Dont la meſure eſt racourcie, autant, que la ligne ſemble eſtre plus longue.
-|- style="font-family: times, serif; vertical-align:top"
-|In sum, these considerations do not diminish the worth of this Circle, as much as they improve it. Because these same difficulties, which are proposed against it, clarify the concurrence with Nature itself, to which our ideas must always refer.
-|En fin, ces conſiderations ne diminuent pas l’eſtime de noſtre Cercle, ains elles l’augmentent; puis que les difficultez meſmes, qui ſont propoſées alencontre, en eſclarciſſent davantage la convenance avec la Nature meſme, à laquelle il faut que toutes nos inventions ſe raportent.
-|- style="font-family: times, serif; vertical-align:top"
-|So, to make it easier to remember, here is a Table of measurements of all these Instances and their differences. To begin, for the Lateral Instances, there are
-|Or pour vous en confirmer d’autant plus la memoire, voicy un Tableau de la meſure de toutes ces Inſtances aved leurs aggrandiſſements. Et premierement pour les Inſtances Laterales, il y a
-|- style="font-family: times, serif; vertical-align:top"
-|First Instance<font style="text-align: right">About 26.48 Spans </font>
-|Pour la Premiere <font style="text-align: right">Nombres 26,48@ </font>
-|- style="font-family: times, serif; vertical-align:top"
-|Second Instance <font style="text-align: right">About 22.45 Spans</font>
-|Pour la Seconde <font style="text-align: right">Nombres 22,45@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Third Instance <font style="text-align: right">About 19.45 Spans</font>
-|Pour la Troiſieme <font style="text-align: right">Nombres 19,45@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|For the Instances on the Diameter:
-|Touchant les Inſtance Diametrales:
-|- style="font-family: times, serif; vertical-align:top"
-|First Instance <font style="text-align: right">About 26.48 Spans</font>
-|Pour la Premiere <font style="text-align: right">Nombres 26,48@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Second Instance <font style="text-align: right">About 22.17 Spans</font>
-|Pour la Seconde <font style="text-align: right">Nombres 22,17@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Third Instance <font style="text-align: right">About 18.48 Spans</font>
-|Pour la Troiſieme <font style="text-align: right">Nombres 18,48@</font>
-|- style="font-family: times, serif; vertical-align:top"
-|As for the tip of the sword, how far it must travel to hit the adversary’s body:
-|Et touchant la pointe de l’eſpee, combien qu’il faut qu’elle chemine, pour toucher le corps contraire:
-|- style="font-family: times, serif; vertical-align:top"
-|From the First Instance <font style="text-align: right">One Arms Length</font>
-|A la Premiere <font style="text-align: right">La longeur de bras.</font>
-|- style="font-family: times, serif; vertical-align:top"
-|From the Second Instance <font style="text-align: right">One Forearm</font>
-|A la Seconde <font style="text-align: right">Vne coudee.</font>
-|- style="font-family: times, serif; vertical-align:top"
-|From the Third Instance <font style="text-align: right">A half-palm</font>
-|A la Troiſieme <font style="text-align: right">Vne demi paulme.</font>
-|- style="font-family: times, serif; vertical-align:top"
-|Those who are curious and wish to check these calculations, will find them mathematically accurate, and for those who are only interested simply for practical use can measure the ground. Use a stick as long as the Diameter divided into 24 Spans, each Span divided into 10 Parts, and each Part divided into 10 Minutes. Checking the aforesaid lines against this stick, they will find the correct measurements for our Instances, and by this can be assured of the accuracy of several observations that shall be set out, below.
-|Ceux qui ſeront curieux d’examiner ces calculations de plus pres, les trouveront aſſez accordantes aux regles de la Mathematique, & pour ceux qui n’en quierent que la ſimple Pratique, ils en pourront prendre la meſure ſur le terroir avec un baſton de la longeur du Diametre parti en 24.Nombres, & chaſqun d’icieux nombres en 10.parties, & les parties on 10.minutes. En appliquant lequel ſur leſdites lignes, ils recognoiſtront les juſtes meſures de nos Inſtances, & par icelles ſe pourront aſſeurer de la certitude de pluſieurs obſervations, qui ſeront propoſées cy apres.
-|- style="font-family: times, serif; vertical-align:top"
-|As for the rest, be advised that, for all practical use, the lines will be enough to provide proper alignments and ranges, even without calculations.
-|Au reſte on vous advertit, qu’on ſe peut contenter en la Pratique de la ſeule meſure des lignes, qui donneront aſſez d’adreſſe d’elles meſmes, encores qu’elles ne ſoyent pas calculées.
-|- style="font-family: times, serif; font-size: 20pt; vertical-align:top"
-|'''Circle No 5'''
-|'''Cercle N.5'''
-|- style="font-family: times, serif; vertical-align:top"
-|''Showing the concordance of the Circle, & of the Instances, with Man’s Movements, and so understand accurately timing & reach.''
-|''Representent la convenance de Cercle, & des Inſtances, avec les Mouvements de l’Homme, pour en cognoiſtre la juſteſſe du Temps, & de leur portee.''
-|- style="font-family: times, serif; vertical-align:top"
-|In the plane of Circle No 5 we first show the proportions of Man, the same as in Circle No 1, even though the figure is inverted, head downwards & feet upwards, to demonstrate that the aforesaid proportions remain the same, whether starting from one end of the Diameter or the other.
-|Au plan de ce Cercle N.5, ſont representées en premier lieu les proportions de l’Homme, toutes les meſmes qu’au Cercle N.1, y eſtant toutesfois la figure de la perſonne renverſée, la teſte embas, & les pieds en haut, pour demonſtrer, que leſdites proportions demeurent jouſiours immobiles, tant à commencer de l’un bout du Diametre, que de l’autre.
-|- style="font-family: times, serif; vertical-align:top"
-|The same figure demonstrates that the distance for the First Instance is equal to the extended height of the person. As well, the distance of the Second Instance is equal the natural stature from sole of the feet to the top of the head. And the distance of the Third to the height of the chest, which is also shown in the preceeding Circle.
-|Il eſt auſſi demonſtré par la meſme figure, que l’intervalle de la Premiere Inſtance, eſt egale à la hauteur eſtendue de la perſonne: Pareillement, que l’intervale de la Seconde Inſtance eſt egale à la ſtature naturelle du corps depuis la plante des pieds juſqu’au ſommet de la teſte: Et l’intervalle de la Troiſieſme à la hauteur de la poitrine, comme auſſi il a eſté demonſtré au Cercle precedent.
-|- style="font-family: times, serif; vertical-align:top"
-|Furthermore, there are three inscriptions running around the circle. The first, running along the entire Circumference, says that one must move the entire arm when striking from the First Instance. The second, which is the middle one, says one need only move from the elbow to do the same from the Second. And the third, which likewise corresponds to the Third Instance, that from here one need only use the wrist. For as much as it requires effort to raise the sword and arm up high, when the body stays withdrawn, as it is in the First Instance. When the sword descends it moves forward and gets closer but this is with the advantage of natural motion, which is dropping to break and counter all the adversary’s initiatives. But in the Second and Third Instances, the body is so close that if he were to move his entire arm, he would be entrely uncovered and completely give the initiative to his adversary, which would be wholly inevitable danger, were he to try it. And so, in the one only the movment of the elbow can be allowed and in the other no more than the wrist.
-|Il y a davantage en ceſty cy trois eſcriteaux, qui vont en rond. Le premier, coſtoyant toute la Circonference, & ſignifiant qu’il eſt loiſible de mouvoir le bras entier, pour mener ſur l’Ennemi un coup de taille depuis la Premiere Inſtance. Le ſeconde, qui eſt celuy du milieu, contient en ſubſtance, qu’on ne doit mouvoir que le coude tant ſeulement, pour faire le meſme à la Seconde. Et le troiſieſme, qui reſpond pareillement ſur la Troiſieſme Inſtance, qu’en icelle on ne le peut faire, ſinon ſeulement du poignet de la main. Car encore que l’eſpee & le bras montent en haut avec un movemēt violent, ſi eſt ce que le corps demeure eſloigné tandis qu’il eſt en ſa Premiere Inſtance, & quand l’eſpee vient à deſcendre, il s’avance & approche, mais c’eſt avec l’avantage du mouvement naturel, qui eſt baſtant à rompre & dompter toutes les entreprinſes contraires. Mais à la Seconde & Troiſieſme Inſtance le corps eſt ſi pres, que tout autant qu’il ſe deſcouvre, & autant de temps qu’il accorde à ſon Contraire de faire quelque entrepinſe, ce ſont tout autant de dangers inevitables, où il ſe hazarde. Et partant, en l’une il n’eſt permis de mouvoir que le coude, & en l’autre non plus que le poignet.
-|- style="font-family: times, serif; vertical-align:top"
-|The variety of situations comes from the inequality of the spaces between the two Opponents, which means one has more or fewer options to change or modify one’s movements. Which is a general warning to students never to attempt to do anything that he can only succeed in doing by chance. And at all the Distances, where he finds himself, that he holds himself always on guard against beginning something which cannot do confidently. This is worth exploring in more detail.
-|La diverſité procede de l’inegalité de l’eſpace qui demeure entre les deux Contraires, ſuivant laquelle on a plus ou moins de loiſir pour changer où moderer ſes mouvements. Qui eſt un advertiſſement general au diſciple, afin qu’il n’entreprenne jamais de faire, ce qui ne peut reuſſir à bien, que par hazard; & en toutes les Diſtances, où il ſe trouve, qu’il ſe tienne touſiours ſur ſes gardes, pour ne commencer choſe qui ne ſoit conjoinćte avec aſſurance. Or il vaut la peine de declarer ceſte matiere un peu diſtinćtement.
-|- style="font-family: times, serif; vertical-align:top"
-|As I have said, that anyone who would strike from the First Instance must move his tip an entire arm’s length: which is a distance so long that one has ample time to turn the entire arm aside, and even to bring the hand above the head, and to change position in time to interrupt any of the Opponent’s actions before he can move his tip such a long distance.
-|Nous avons dit, que celuy qui nous veut atteindre depuis la Permiere Inſtance, qu’il luy convient avancer ſa poinćte de la longeur entiere de noſtre bras: qui eſt une eſpace ſi grande qu’on y a loiſir de tourner & virer le bras entier, & mener meſme la main par deſſus la teſte, & de changer touſiours à temps pour empeſcher l’effet de l’entreprinſe du Contraire, avant que ſa pointe puiſſe achever une ſi longue courſe.
-|- style="font-family: times, serif; vertical-align:top"
-|In the Second Instance, to hit the opponents body, requires no more than a foot distance and it is inadvisable in such dangerous circumstances to move the hand off the centre-line, as happens when using the entire arm to carry the movement.  Which is why, to guard against surprises one must not make any movements larger than those that come from the elbow, which shall be explored more exactly in the Practical discussion.
-|A la Seconde Inſtance pour toucher le corps contraire, il ne faut qu’environ un pied de longeur, de façon qu’il n’eſt pas loiſible en un danger ſi evident d’eſcarter la main hors de preſence, comme il en advient quant on le transporte avec le movement du bras entier. Parquoy pour s’aſſurer contre les ſurprinſes, il n’y faut point faire de plus grands mouvements, que ne ſont ceux qui procedent du coude, en y apportant meſmes la circonſpećtion requiſe, de quoy ſera parlé plus exaćtement en la Practique.
-|- style="font-family: times, serif; vertical-align:top"
-|In the Third Instance, one can be hit with the smallest move. It is clear that at so close a distance no movement of the sword other than with the wrist can be permitted; for if one opens oneself up, for no matter how small a time, one cannot avoid being hit, if the Opponent takes full advantage of the opening  he is given.
-|A la Troiſieme Inſtance on eſt atteint avec le moindre avancement du monde. Dont il appert clairement, qu’en une ſi petite diſtance il n’eſt aucunement permis de faire autre mouvement avec l’eſpee, que du poignet tant ſeulement: car ſi on ſe forligne, pour peu que ce ſoit, on ne pourra eviter de recevoir l’atteinte, ſi le Contraire prend bonne garde à l’occaſion, qui luy en eſt donnée.
-|- style="font-family: times, serif; vertical-align:top"
-|All that has been said about close hits applies to long, hard strikes. This observation gives us the skill to adjust our timing according to the distance as we approach.
-|Ce que nout diſons de coups de taille, ſoit auſsi entendu à l’advenant des eſtocades. Car c’eſt l’obſervation, qui nous donne l’adreſſe de modere touts les movements à l’advenant du temps.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|On the superiority and elegance of this present circle in this training
-|DE L'EXCELLENCE ET
-dignite de ce present cercle en cest exercice
-|- style="font-family: times, serif; vertical-align:top;"
-|In conclusion, the Circle is the foundation of the science of Arms; it is this that allows us to perceive all the dangers which might present themselves during a fight, guides our movements, focuses our intentions, gives assurance to our steps, and from which proceeds all the rest of the demonstrations that follow, and that we shall use to serve us, during the perilous voyage of our Training, as sailors use a compass and map to avoid the shoals and sandbanks of the sea, and so, in the end, arrive safely in the intended port. All good and secure offence and defence derives from this point of origin and for this good reason it can be called the Key to Training. For just as a key has three jobs: to open, close, and guard, so does this figure, which opens for us the means to attack, and to defend by closing the door to attacks by the Adversary, & furnishes us with protection, like a solid rampart, against all disruptive moves, a job which it accomplishes and effectively guards us, as Practical Training shall prove.
-|Pour concluſion, le Cercle c’eſt le fondement de la Science des Armes; c’eſt celuy qui nous deſcouvre touts les dangers, qui ſe peuvent preſenter par tout le diſcours d’une bataille; guide de nos mouvements, adreſſe des intentions, aſſeurance des pas, duquel auſſi tout le reſte des demonſtrations ſuivantes procede, & duquel on ſe ſervira parmy les perilleuſes vagues de ceſt Exercise, comme les Matelots de la buſſole, & d’une bonne carte Marine, pour eviter les eſceuils & bancs de mer, & en fin parvenir au repos au port qu’ils ſe propoſent. Toute bonne & ſeure offenſion & defenſe prend d’icy ſon origine, en ſorte qu’à bon droit peut il eſtre appellé la Clef de l’Exercice. Car ainſi qu’une clef a trois offices, ſçavoir Ouvrir, Fermer, & Garder, auſſi eſt ce ceſte figure, dont l’uſage nous ouvre la maniere d’aſſaillir & de defendre, ferme la porte aux intentions & entrepinſes du Contraire, & nous munit, comme d’un ſolide rempart, contre touts ſes mouvements deſordonnez, en quoy elle accompit l’office & l’effećt de nous contregarder; ainſi que la Pratique en fera l’eſpreuve.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|On the correct lentgh of the sword, which everyone should carry for defence, based on one’s own limbs.
-|De la iuste longueur de l’espee, qve chascvn doit porter pour sa defense, accordant avec les membres de son corps.
-|- style="font-family: times, serif; vertical-align:top;"
-|Enough has been said describing the Circle. Now let us turn our attention to the Sword and it’s correct length, which is proportional and fits with all movements of the human body, and is consequently the best size of all.
-|A tant ſoit aſſez dit de la declaration du Cercle. Parlons maintenant de l’Eſpee, & de ſa juste longeur, qui ſoit proportionée & convenable à touts les mouvements du corps humain, & par conſequent auſsi la meilleure de toutes.
-|- style="font-family: times, serif; vertical-align:top;"
-|It is amazing how, among those who make a living in the profession of Martial Arts, and who have published writings to the world, so few concern themselves with this matter, principally because this comes up in the constant discussions on the advantages of longer or shorter swords against each other, and because all confidence concerning timing and range, the two most important aspects of Training, depends absolutely on this knowledge, and because we use the sword to execute almost every move, in attack as in defence, it must follow that if the range and size are not well known, all moves become uncertain and hazardous.
-|C’eſt merveille, qu’entre ceux, qui ont fait tout le temps de leur vie profeſsion des Armes, & en ont publié des eſcrits parmy le Monde, il s’en trouve ſi peu qui touchent à ceſte matiere: & principalement puis qu’il ſe preſente journellemēt à diſcourir touchant l’avantage des eſpees longues ou courtes les unes contre les autres; & que de ceſte ſeule cognoiſſance depend toute laſſeurance des temps & des meſures, deux parties principales de l’Exercice: & puis que c’eſt l’eſpee, qui fait quaſi ſeule toutes les executions, tant en aſſaut qu’en defenſe, il s’enſuit neceſſairemēt, que la meſure & la portee en eſtant incognue, toutes les operations en deviennent incertaines & hazardeuſes.
-|- style="font-family: times, serif; vertical-align:top;"
-|Nontheless, there are a few who discuss this and who determine proper sword-length, but for the the most part, as cowards, who use very long blades to stay at a distance, than to show any real science of arms. And such is the opinion of those who swear that the length of the blade should be two arms length, so that if the point were put into the ground beside a man, the crosspiece would come to the armpit; which is, in effect, more like the length of the Espadon [great-sword], than a sword: other than this would necessarily be as annoying and inconvenient to wear at the side, as it would be to draw from the scabbard, as it would be dangerous and clumsy to use.
-|Toutesfois il s’en eſt trouvé quelques uns, qui en ont voulu parler, & ont meſmes determiné la meſure de l’eſpee; mais pluſtoſt à l’appetit de quelques couards, qui ſe plaiſent à des armes fort longues, pour demeurer touſiours en diſtance, que par aucune vraye demōſtration de Science. Et telle eſt l’opinion de ceux qui veulent, que les lames doivent eſtre egales à deux bras entiers, de ſorte que la pointe eſtant miſe à coſté de l’homme en terre, le pommeau de la guarde luy vienne à toucher l’aixelle; qui eſt en effet pluſtoſt la longeur d’un Eſpadon, que d’une Eſpee : outre ce qu’elle ſera neceſſairement auſsi malfeant et incommode, tant à porter au coſté, que pour tirer hors du fourreau, comme dangereuſe & peu manniable en l’uſage.
-|- style="font-family: times, serif; vertical-align:top;"
-|Leaving aside for the moment all other considerations which we could bring up on the subject of the correct size of the Sword, besides those of the most convenient and advantageous use and handling, I will say that there are times when a longer or shorter sword is better. And yet, to answer the question as to determine a length, it should be between these two extremes, in the middle; not too short against long swords, nor likewise too long against short swords, and such that it is always easy to handle however one wishes. And because of this, as it means that the length should be proportional to the person, we have taken the size from his own body. Everyone should have his weapons sized proportionally to their own person. Thus the size of the Sword should be such that the length of the blade from the tip to the crosspiece is equal to half the Diameter, that is to say, if the tip is placed on the ground between the feet, the crosspiece of the handguard will come up to the navel, just as explained in Circle No 1, and the more exactly one can achieve this, the better, for many reasons. So there are ten small figures, labelled with letters A to K along the edges of the Plate, which will serve, for now, as a practice guide; the meaning of these follows.
-|Laiſſant donc preſentement à coſté toutes autres conſiderations, qu’on pourroit mettre en avant touchant la vraye Meſure de l’Eſpee, horsmis celle de l’uſage & du maniement le plus commode & le plus avantageux, je di, qu’il y a des occaſions plus favorables pour les eſpees longues, & des autres qui le ſont plus pour les courtes. Et par tant s’il eſt queſtion de luy aſsigner une meſure, qu’il la faut mettre entre les deux extremes, ſi bien qu’elle ſoit mediocre; non trop courte contre les eſpees longues, ne pareillemēt trop longue contre les eſpees courtes, & qu’elle ſoit en toutes occaſions maniable à ſouhait. Et puis qu’il faut neceſſairement qu’une telle longueur ſoit proportionnée à la perſonne meſme, nous l’avons tirée & demonſtrée hors de la meſure de ſon corps; & voulons que chaſcun ait ſes armes proportionnée à l’advenant de ſa propre perſonne. Dont la meſure de l’Eſpee ſera telle, que la longueur de ſa lame depuis la pointe juſques à la croiſee, ſoit egale au demi Diametre; c’eſt aſſavoir, que la pointe eſtant miſe en terre entre le creux de ſes deux pieds, les branches de la garde luy viennent à reſpondre juſtement ſur la haueur de nombril; cōme il ſe voit exprimé au Cercle N. 1. Et le plus exaćtement qu’on le pourra pratiquer, ce ſera le meilleur, pour diverſes raiſons; dont nous avons mis icy par proviſion des dix petites figures, marquées de lettres ſuivant l’ordre alphabetique depuis l’A juſques au K au long des bords du Tableau, qui en ſerviront pour le preſent de preuve: & en eſt la ſignification telle que s’enſuit.
-|- style="font-family: times, serif; vertical-align:top;"
-|In any case, before the explanation, you should know that the proportions of the images of these people represented by the said figures, are drawn from and adjusted to the measure of the two small Circles I & K set on the plane of the pavement at the bottom of the Table. About this, if there arise any doubts, and to be entirely certain, one may measure the figures with a compass, and find the natural body height of each of these persons will be the same as the line C-V; the size of their swords, like the half Diametre; and the length of their arms, like C-H.
-|Toutesfois avāt l’explication je vous adverti, que le proportions des images de ces perſōnes repreſentées par leſdites figures, ſont tirées & adjuſtées ſur la meſure de ces deux petits Cercles I & K, couchez ſur le plan du pavé au bas de la Table. Touchant quoy, pour en avoir pleine intelligence, & pour l’explictation des doutes, qui en pourrouyent ſourdre, il ſera expedient de les meſurer au compas. Car la hauteur naturelle des corps de caſcune de ce dites perſonnes ſera comme la ligne CV; la meſure de leurs Eſpees, comme le demi Dimametre; & la longeur du bras, comme CH.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure A
-|Figvre A
-|- style="font-family: times, serif; vertical-align:top;"
-|To begin with Figure A, here we see that the length that we have determined for the sword does not bother anyone, whether in casual conversations, or in a crowd, or moving through narrow passages, or similar situations where one would ordinarily be encumbered by a sidearm. On the contrary, with a blade of this length, and in a belt and hanger, of a design which we shall show in the following Plate, drawing the handle towards oneself with the right hand,  the point by itself falls perpendicularly to the ground beside the person, the hilt a little forward, together with the handle falls in its proper place, on the hip, at the height of the navel, when one moves the left foot a half-pace forward, one can comfortably rest the elbow and in fact the left side on it; as such it serves as a rest, rather than an encumbrance like all other swords not proportionally sized.
-|Pour le premier il eſt repreſenté par ceſt figure A, que la longueur, que nous mettons pour l’Eſpee, ne donne point de faſcherie à la perſonne, quād on eſt en converſation avec des gens, ou qu’on ſe trouve en la foule, ou cheminant par des eſtroits paſſages, ou en ſemblable occaſions, eſquelles on eſt ordinairement embaraſſé par les armes qu’on porte. Au contraire eſtant la lame de ceſte longueur, que nous luy avons aſsignée, & la portant à coſté avec un tel ceinturon & pēdant d’eſpee, qu’il ſera domonſtré en la Table ſuivante, moyennant qu’on tire la garde devers ſoy avec la main droite, la pointe viendra à tomber d’elle meſme perpendiculairement en terre à coſté de la perſonne, un peu devant, enſemble auſſi la garde en viendra à ſe mettre en ſa juſte place, ſi bien à point, & à l’egal de la hauteur du nombril, qu’en avançant le pied gauche environ d’un demi pas, on aura la commodité de repoſer le coude, & enſemble tout le coſté gauche du corps deſſus; en ſorte qu’elle ſervira d’un appuy, pluſtoſt que de nous empeſcher, comme font neceſſairement toutes les eſpees, qui n’ont pas la longueur proportionée.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure B
-|Figvre B
-|- style="font-family: times, serif; vertical-align:top;"
-|The same length of sword is also very convenient for drawing the blade. For, as shall be explained in the next Table, and as the Circle itself shows, when carrying the sword on a belt & hanging as described, the guard comes slightly forward beside the hip, the scabbard angles towards the rear; each at its correct height, and so one may easily use both hands at the same time, with the left hand grips the scabbard just below the guard and the right hand reaches circularly across in front to grip the handle, in a way that requires no other preparation, no twisting the body, as we ordinarily see done by others, as if they had to search for their sword, or as if it were not properly attached to their side, a very clumsy, if common, arrangement.
-|La meſme longueur d’eſpee eſt auſſi tres commode pour le deſgainement. Car en la portant avec le ceinturon & le pendent de noſtre deſcription, qui ſera propoſé au prochain Tableau ſuivant, & que le Cercle meſme demonſtre; la garde en vient un peu en avant à coſté du corps, le fourreau tirant vers le derriere; chaſcun en ſa juſte hauteur, & en telle ſorte qu’on peut travailler à ſon aiſe en un meſme temps de la main droite & de la gauche, en portant la main gauche embas, pour empoigner le fourreau pres de la garde, & la droite circulairement en avant, pour prendre l’eſpee, ſans aucune autre preparation, ne ſans courber le corps, comme on voit faire ordinairement aux autres, quaſi comme s’il la falloit cercher, ou qu’elle ne fuſt aſſez à commandement attachée au flanc de celuy qui la porte. choſe qui  eſt de tres mauvaiſe grace, encor qu’elle ſoit assez commune.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure C
-|Figvre C
-|- style="font-family: times, serif; vertical-align:top;"
-|Next we see the operation of drawing the sword, which, we shall describe more fully in Plate III  with all the various circumstances and reasons for which, in drawing the sword, one is constrained to raise one’s hand and arm as high as possible, even to raise the right leg, or any other bodily action, which may even include opening the fingers, to raise the hand sufficiently to clear the scabbard. All of which are necessary to assist in drawing because of the length of the blade. Thus it is apparent that our size of blade is so large that it could not be made longer without causing considerable inconvenience.
-|S’enſuit l’operation meſme du deſgainement, que nous deſcrirons plus particulierement au Tableau III. avec toutes ſes circonſtances, & les raiſons, pour leſquelles en faiſant le deſgainement on eſt contraint de hauſſer le bras, enſemble avec la main, tant qu’il eſt poſſible, meſmes de lever auſſi la jambe droite, & d’accomoder toutes les aćtions du corps, à celle fin que la main puiſſe monter à ſuffiſance, pour laquelle meſme conſideration il convient auſſi ouvrir les doigts. Leſquelles choſes ſont toutes neceſſaires à cauſe de ceſte longueur de la lame, qui a beſoin d’eſtre aſſiſtée de toutes ces aides. Dont it appert que noſtre meſure de lame eſt ſi grande, qu’elle ne pourroit eſtre de plus ſans des notables incommoditez.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure D
-|Figvre D
-|- style="font-family: times, serif; vertical-align:top;"
-|So, as this blade length is equal to the lower half of the extended body, from the soles of the feet to the navel, it is also equal to the upper half, from the navel to the highest that the hand can be raised above the head and as we see from the figure these two halves are equal. This is easy to show, as it is here. If we put the tip on the ground with one end of the crosspiece on the navel, and rotate the the tip upwards around the crosspiece, one will find the tip is as high as one’s fingers can reach.
-|Or tout ainſi que ceſte meſure eſt egale à la partie inferieure du corps eſtendu, depuis la plante des pieds juſqu’à la hauteur du nombril, auſſi l’eſt elle pareillement à la partie ſuperieur, depuis le nombril en ſus juſques au plus haut que la main peut atteindre, comme on voit en la figure que ces deux parties ſont egales en longeur; auſſi la preuve en eſt facile, comme elle eſt icy repreſentée. Car en mettant la pointe de l’eſpee en terre avec l’une des branches de la croix ſur le nombril, & tournant en apres la pointe droitement en haut, l’on trouvera, qu’elle viendra au plus haut qu’on pourra toucher du bout des doights.
-|- style="font-family: times, serif; vertical-align:top;"
-|And thus it can be seen once again, that the size of the blade is equal to half of the extended length of a person, and equal to the radius of our Circle, taking the navel for the Centre and the extended length as the the Diameter.
-|Et voilà comme il appert derechef, que la meſure de la lame eſt egale à la juſte moitié de la longueur eſtendu de la perſonne, & pareillement au demi-Diametre de noſtre Cercle, prenant le nombril pour le Centre, & la longueure eſtendue pour le Diametre.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure E
-|Figvre E
-|- style="font-family: times, serif; vertical-align:top;"
-|As for the natural height of a person from the soles of the feet to the top of the head, this can also be measured and is here shown to be measured with the sword. For if we grip the handle in the style of our training, about which we shall discuss more later,  and one extends the sword and arm in a straight line, as we can see with one of these two persons, keeping the tip, the guard, and the shoulder at the same height, the line of the sword and arm, from the tip to the shoulder or the armpit, will be found to be equal to the height of the person. If one wishes proof, take a long stick or half-lance, and measure the distance from the tip of the blade to the armpit, then place the end of the stick on the ground between the feet and and stand it upright. It will be found that the measurement is exactly the size of the person.
-|Quant à la hauteur naturelle de la perſonne depuis  la plante des pieds juſques au ſommet de la teſte, icelle ſe peut auſſi meſurer, & eſt icy repreſentée à meſurer avec l’eſpee. Car ſi on la prend au poing ſuivant le ſtile de ceſtuy noſtre Exercice, dont il ſera parlé cy apres, & qu’on l’eſtende enſembe avec le bras en droite ligne, ainſi qu’il ſe voit en l’une de ces deux perſonnes, tenant la point, & la garde, & l’eſpaule en egale hauteur; la ligne de l’eſpee avec le bras, depuis la pointe de la lame juſques à l’eſpaule ou à l’aixelle, ſera trouvée egale à la ſtature de la perſonne. Si vous en demandez la preuve, prenez un long baſton ou un demie lance, et en meſurez de longeur depuis la pointe de la lame juſques a l’aixelle: puis appliquez ceſte meſme ligne à la hauteur de la perſonne, mettant le ſuſdite baſton entre le creux de ſes deux pieds, & le dreſſant tout drout contre le corps pour le meſurer. Et ce faiſant ſera trouvé, que la meſure en accordera juſtement à la hauteur de la perſonne.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure F
-|Figvre F
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps"
-|SHOWING HOW
-the when the body is erect and in profile, the arm and sword extended in a straight line, the reach is further than any other.
-|DEMONSTRE QV'ESTANT LE
-corps perpendicvlaire et en povrfil, le bras et l’espee estendvs en droite ligne, atteignent plvs loing qv’avtrement
-|- style="font-family: times, serif; vertical-align:top;"
-|Now we shall prove that this same length of sword can be increased or shortened, according to the reach of various distances, depending on where one is. This is shown by the three following figures, F, G, & H, the first of which, marked F, shows how the arm and sword extended out in a straight line is the longest reach of all positions, as long as the body position does not change, of course. If one stands erect on both legs, neither leaning forwards, nor backwards, and one extends the sword and straightens the arm in a line, that is, with the tip and the guard at shoulder height, one will reach further forward than if one raises or lowers the tip. For one cannot do either without the tip following a curve along a circumference, which is also shown in the figure. By which it is evident that the more the tip rises or lowers, the further it moves from the nearest point of contact.
-|Maintenant nous proverons, que ceſte meſme longueur d’eſpee eſt capable de s’allonger, & de ſe raccoucir, ſelon la meſure des diſtances, où on ſe trouve. Ce que nous ferons paroiſtre par les trois figures ſuivantes, F.G.H. dont la premiere, qui porte la marque d’un F. repreſente, que la droite ligne, qu’on fait avec l’eſpee & le bras eſtendu, eſt la plus longue de toutes celles qui peuvent eſtre faites avec ladite eſpee, à condition toutesfois, que le corps demeure en une meſme poſture. Car ſi on ſe tient droit ſur ſes jambes, ſans que le corps s’avance, ne ſe recule,  & qu’on eſtende le bras avec l’eſpee en droite ligne, c’eſt à dire, mettant la garde & la pointe juſtement en la hauteur de l’eſpaule; on attendra plus avant, que ſi la pointe monte, ou qu’elle s’abaiſſe. Car elle ne peut faire ne l’un ne l’autre, ſinon en allent courbe, à la maniere d’une circonference, comme il eſt auſſi repreſenté en la figure. Par la quelle il eſt evident, que d’autant plus que la pointe continue à monter ou à deſcendre, d’autant plus elle s’eſcarte du plus prochain endroit de l’attouchement
-|- style="font-family: times, serif; vertical-align:top;"
-|To be more precise, we divide the blade into 12 Spans, with the length of the arm at about 8 Spans, and the elbow, which is almost in the middle of the arm, at about 4 Spans long. So, the blade can rise or descend in a circular arc three ways; through the movement of the entire arm, by the movement of the elbow, or by the movement of just the wrist. It follows in the first case when one moves the entire arm, that the centre of this circle is at the shoulder, and consequently, the radius, which determines this arc of circumference, rising or descending, is the line of the sword together with the entire arm, which together equals about 20 Spans. In the second case, moving from the elbow, the centre is at the elbow, the length of the radius is 12 Spans plus 4 Spans, which together makes 16 Spans. In the third case, when one moves only from the wrist, the centre is the person’s fist, only the blade moves, which makes a radius of 12 Spans. Now everyone, with any knowledge of mathematics, knows that the circumference of a circle is proportional to its radius: and these become shorter; also, therefore a radius of 20 is greater than 16, and that of 16 greater than the third which is 12. It follows that, raising or lowering the tip with just the wrist, shortens our distance to the tip, more than if one uses the elbow, and with the elbow likewise more than using the entire arm.
-|Pour en parler plus exaćtement, ſachez que nous partiſſons la lame in 12. Nombres, dont la meſure du bras en contient auſſi environ 8. en ſorte que le coude, qui en eſt quaſi la juſte moitié, en revient comme à 4. Nombres. Or eſt il que la pointe de l’eſpee peut monter ou deſcendre circulairement en trois ſortes; aſſavoir par le mouvement du bras entier, par le mouvemēt du coude, ou par le mouvement du ſeul poignet de la main.  Dont il s’enſuit au premier ſens quand on fait le mouvement du bras entier, que le centre d’iceluy giſt en l’eſpaule, & par conſequent, le demi-Diametre, qui doit faire la ſuſdite circonference, montante ou deſcendante, c’eſt la ligne de l’eſpee enſemble avec le bras entier, qui font enſemble bien pres de 20. Nombres. Et au ſecond, en faiſant le mouvement du coude, le centre eſtant au coude, la longueur de la ligne totale contient 12. & 4. qui font enſemble 16. Et pour le troiſieme, quand on fait le mouvement du ſeul poignet, le centre eſtant le poing de la perſonne, il n’y a que la lame ſeule, qui fait 12. Nombres pour la ligne du demi-Diametre. Maintenant chaſcun, qui a quelque intelligence des Mathematiques, ſçait que les circonferences ſont proportionelles à leurs demi-Diametres: & que les circonferences ſe raccourciſſent à l’advenant: & partant puis que le demi-Diametre 20. eſt plus grand que celuy de 16. & celuy de 16. plus grand que le troiſieme de 12. il s’enſuit qu’en hauſſāt ou abaiſſant la pointe, du poignet de la main tant ſeulement, on raccourcit le chemin de la pointe, qui eſt la circonference plus, qu’on le faiſant du coude: & avec le coude pareillement plus, qu’en faiſant le mouvement avec le bras entier.
-|- style="font-family: times, serif; vertical-align:top;"
-|It would be very easy to mathematically calculate the differences of distance, but it is enough to show only one small example, from which it will be very simple to understand the rest that follows.
-|Il ſeroit bien aiſé de calculer par raiſon Mathematique, combien ces differences portent: mais il nous ſuffira d’en propoſer ſeulement un petit exemple, par le quel is ſera facile d’entendre auſſi à l’advenant le reste.
-|- style="font-family: times, serif; vertical-align:top;"
-|Take the case where the tip of the sword is raised using just the wrist, so that the centre of motion is the hand, and consequently the radius is only the length of the sword, making 12 Spans and suppose the tip rises likewise a distance of 12 Spans along the circumference; drop a line perpendicularly from the tip to the ground and one will find the line 12 Spans long shortened by 6 Spans, that is, by half.
-|Poſons donc le cas, qu’on hauſſe la pointe de l’eſpee du ſeul poignet; en ſorte que le centre de l’aſcenſion ſoit en la main, & par conſequent le demi-Diametre ſoit la ſeule longueur de la lame, faiſant 12. & que la pointe monte pareillement en circonference à 12. Nombres en haut; alors en laiſſant deſcendre une ligne perpendiculare du lieu de la pointe vers la terre, on trouvera, que la ligne 12 ſera raccourcie de 6. Nombres; c’eſt à dire, de la juſte moitié.
-|- style="font-family: times, serif; vertical-align:top;"
-|If the tip rises by only 6 Spans, which is half of the previous rise, one finds the line shortened by only 1½ Spans, or one quarter the previous distance.
-|Si la pointe ne monte, que 6. Nombres, qui eſt la moitié de l’aſcenſion precedente, on trouvera par la ligne perpendiculaire, qu’ell ſera racourcie de 1½, qui n’eſt, que le quart du precedent raccouciſſement.
-|- style="font-family: times, serif; vertical-align:top;"
-|If it rises only 3 Spans, the line will again be shortened by one quarter of the previous distance or ¾ Spans.
-|Si elle ne monte qu’à 3. Nombres de hauteur, la ligne du raccouriſſement ſera derechef le jusſte quart du precedent, aſſavoir ¾.
-|- style="font-family: times, serif; vertical-align:top;"
-|Likewise the same happens when we raise the tip from the elbow. Because if the tip rises 16 spans, the distance shall be shortened by 8. If raised up to 8 Spans, it will be shorter by 2. And if it is raised by only 4, it will be shorter by ½, which is only a quarter of the preceeding step.
-|Ainſi en eſt il pareillement des autres aſcenſions, mettent le centre ſur le coude. car ſi la pointe en monte à 16. Nombres, elle ſe raccoucira de 8. Si juſques à 8. Nombres, elle s’en racourcira de 2. Et ſi elle ne monte qu’à 4. elle en ſera raccourcie ½, qui n’eſt que le quart du precedent.
-|- style="font-family: times, serif; vertical-align:top;"
-|Of course the same happens when the motion is done with the entire arm.
-|Il faut entendre auſſi le ſemblable des mouvements qui ſe font avec le bras entier.
-|- style="font-family: times, serif; vertical-align:top;"
-|Thus this is the difference between the straight  line versus the other lines at different heights, and we have not even considered  shortening the reach either by bending the arm, or changing the posture, or even simply moving the feet. For there is no doubt that one can reach further than the straight line, if one leans the body forward, or one steps forward: this is not apropos, and beyond doubt, because in such a case, there are two lines, not one, because the extension of the arm with the sword is one line, the movement of the body is yet another. That these two lines together reach further than just the straight arm line alone is not the point. Because to comprehend the reach of each line, we must compare and consider each one independently. To do this, we must leave the body in its natural posture, so as not to skew one way or the other.
-|Voilà doncques la difference de la droite ligne contre les autres, qui ne demeurent pas en egale hauteur; ſans toutesfois conſiderer pour le preſent le raccourciſſemēt, ne la courbure du bras, ne la changement de la poſture du corps, moins encore l’avancemēt qu’il peut faire moyennant la demarche des pieds. Car is ne faut pas douter, qu’on puiſſe atteindre plus loing que la droite ligne, ſi on panche le corps ſur le devant, ou qu’on l’avance avec le demarche: ce qui eſt hors de ce propos & hors de doute, à cauſe qu’en tel cas, il ſe trouve deux lignes contre une, car l’extenſion du bras avec l’eſpee font une ligne, l’avancement du corps en fait encor une autre. Que ces deux lignes, eſtans jointes par enſemble, ſoyent plus longues que la droite ligne ſeule, celà ne touche pa à ceſte queſtion. Car pour ſçavoir la portee de chacune ligne à part, il les faut conſiderer & comparer les unes aux autres diſtinćtement. Et pour ce faire il convient, qu’on laiſſe le corps en ſon eſtat naturel, qui ne favoriſe non plus l’une, que l’autre.
-|- style="font-family: times, serif; vertical-align:top;"
-|Which is why, should one with to confirm the above, stand straight on both feet, hold the sword with the arm outstretched in a straight line, as shown in the figure, just touching the tip to a wall, or some other object at shoulder height, and then raise or lower the tip, with the entire arm, with the elbow, or with just the wrist; without any doubt in the world, you will find your line shortened, more or less, to the degree the centre of motion is more or less distant from the tip as it moves along the circumference.
-|Parquoy ſi vous avez envie de faire preuve de ce que deſſus, mettez vous droit ſur vos pieds, & tenez premierement l’eſpee avec le bras eſtendus en droite ligne, en la maniere qu’il eſt icy repreſenté par la figure, en touchant de la pointe un certain endroit d’un mur, ou de quelque autre corps que ce ſoit ſur la hauteur de l’eſpaule; & puis eſſayez de monter ou d’abaiſſer voſtre pointe, avec le bras entier, ou avec le coude, ou avec la main tant ſeulement; il n’y a point de faute, le moins du monde que vous la montiez ou deſcendez, vous troverez voſtre ligne raccoucie, plus ou moins, au rebours que le centre du movement ſera plus ou moins eſloigné de la pointe, qui fait la circonference.
-|- style="font-family: times, serif; vertical-align:top;"
-|Part of the reason for this difference is when moving the entire arm from the shoulder, the line stays straight, notwithstanding it may move off the most direct path: but when moving from the elbow, one makes an angle, which is, of necessity, a break in the line: and it must also follow that this makes it ever shorter as it moves from the straight line. But as this break angle increases as it moves to the middle, as well as when one performs the moves with the hand, there is yet more shortening: for when the angle is close to the extremity of the line, there is but a small part which draws from the straightness.
-Dont il s’entend auſſi, qu’elle s’accourcira encor d’avantage, en cas qu’on y face deux courbures, l’une ſure le coude, & l’autre ſur le poignet de la main.
-Of course this shortens even further when faced with two bends, one at the elbow, the other on the wrist.
-|La cauſe de ceſte difference giſt auſſi en partie, en ce que quand le mouvement ſe fait avec le bras entier, eſtant le centre en l’eſpaule; la ligne droit demeure en ſon entier ſans aucune courbure, nonobſtant qu’elle forligne quelque peu de la droite voye: mais quand on le fait avec le coude, on fait un angle, qui eſt necessairement une encogneure ſur la ligne: dont s’enfuit auſſi neceſſairement, qu’elle s’accourcit d’avantage, entant qu’elle s’eloigne plus de la droiture. Que ſi ceſte encoigneure de l’angle approche encor plus du milieu de la ligne, ainſi qu’il en advient quand on fait le mouvement avec la main, il y a touſiours encor plus d’accourciſſement; car quand l’angel eſt environ les extremitez de la ligne, il n’y en a qu’une petite partie qui s’esloigne de la droiture.
-|- style="font-family: times, serif; vertical-align:top;"
-|This straight line is of very great use in Training, and shall be the basis for several observations; as such it is worth being carefully described, and well understood. It is the longest and surest of all positions, the most capable in defense of holding off the Enemy at a distance, and the most powerful way to hit offensively. And above all, the straight line can reach the closest target most securely, and without fear of also being struck at the same time. This is why one must always take care to keep this position foremost in training.
-|Ceſte droite ligne aura un fort grand uſage en noſtre Pratique, & ſera le fondement de pluſieurs obſervations, de ſorte qu’elle merite d’eſtre curieuſement declarée, & bien entendu. C’eſt la plus longue & la plus ſeure de toutes, la plus capable en defenſe à tenire l’Ennemi eſloigné, & la plus puiſſante en offenſion pour l’atteindre. Et ce pour autant, que celuy qui en donne l’atteinte au plus proche endroit d’attouchement, il le fait à ſeur, ſans aucun danger de recevoir au meſme temps la pareille. Et pour ceſte cauſe, il faudra touſiours taſcher de s’en prevaloir en la Pratique.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure G
-|Figvre G
-|- style="font-family: times, serif; vertical-align:top;"
-|Nevertheless there are times when one finds oneself in close, where the long lines are useless and even damaging, because the distances are entirely too short for a blade held out at arms length in a straight line (where one must shorten the arm, or even draw it back, to be able to use the tip.) At these close distances the length of our blade is not always comfortable and sufficiently easy to use: so we must shorten the line to  close distances as it is to reach at longer ones. This is what is shown by the following two figures; the one marked G demonstrates how one may shorten the line, if the ennemy runs up to get past the tip, by stopping him with your foot and firmly placing the guard against the right hip, the tip will just reach his chest, which would otherwise pass beyond the shoulder if the sword were longer.
-|Neantmoins quand c’eſt qu’on entre en meſure etroite, où toutes les lignes longues ſont inutiles, & dommageables, à cauſe que les diſtances y ſont aucunefois plus courtes, que les lames eſtendues avec le bras en droite ligne (dont on eſt contraint de raccourcir le bras, ou meſmes de le retirer arriere, afin de ſe pouvoir ſervir de la pointe.) En ces meſures eſtroites noſtre longueur d’eſpee ne laiſſe pas d’y eſtre touſiours commode & maniable à ſuffiſance: car elle eſt autant propre pour raccourcir ſa ligne en ladite meſure eſtroite, qu’elle eſt capable de l’allonger en la grande. C’eſt ce qui eſt repreſenté par les deux figures ſuivantes; dont celle qui eſt marquée de la lettre G. demonſtre comment on la peut raccourcir, en cas que l’Ennemi nous veuille courrir ſus, pour venir au dedans de la pointe. car en luy mettant le pied contre le corps, & affermiſſant la garde ſur la hanche droite, la pointe luy en viendra juſtement devant la poitrine, qui luy paſſeroit autrement par deſſus l’eſpaule, en cas que l’eſpee fuſt plus longue.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure H
-|Figvre H
-|- style="font-family: times, serif; vertical-align:top;"
-|This same shortening can be accomplished another way, by placing the left hand firmly against the chest instead of using your foot, again firmly placing the guard against your right hip, because between the hip and the extended left hand is just enough space to comfortably use the sword as needed.
-|Ce meſme accourciſſement de ligne ſe pourra pratiquer encor en une autre ſorte, en luy mettant la main contre la poitrine, au lieu de ſe ſervir du pied, en affermiſſant derechef la garde de l’eſpee ſur la hanche droite, car entre ladite hanche, & la main gauche eſtendue, il reſtera juſtement l’eſpace de la longueur de l’eſpee, pour la commodité de la manier & appliquer ſelon l’exigence.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure I
-|Figvre I
-|- style="font-family: times, serif; vertical-align:top;"
-|This length of sword is also equal to the double-length step, which is the longest one a person can make without losing power, as shown in Figure I. Since we declared the length of the blade equal to one half-diameter, we can estimate that the step, which is shown along the half-diameter, is also understood to be the length of the blade. Place the toes of the left foot on the letter X, it is impossible for a man to pass beyond the centre in one single step, unless he raises the heel and puts his weight over his right toes, as shown here. Doing this is not a single step with one foot, but two: since both feet move forward, one more, the other less.
-|Ceſte longueur d’eſpee eſt auſſi egale à la longueur du pas double, qui eſt leplus grand que la perſonne puiſſe faire de toute ſa force, ainſi que la Figure I le demonſtre. Car puis que nous ordonnons la longueur de la lame à l’egal du demi-Diametre: il faut eſtimer que le pas, qui eſt representé ſur la ligne du demi-Diametre, s’entend auſſi eſtre fait ſur la longueur de la lame. Mettant donc les orteils du pied gauche ſur la lettre X, je di, qu’il eſt impoſſible à l’homme de paſſer en un ſeul pas outre le centre, ſi ce n’eſt qu’il y accommode auſſi l’autre pied, en eſleveant le talon, & y ſouſlevant le corps ſur les orteils; comme on le voit icy exprimé. Quoy faiſant, ce n’eſt point le pas d’un pied ſeul, mais de deux: à cauſe que tous les deux s’avancent, l’un plus & l’autre moins.
-|- style="font-family: times, serif; vertical-align:top;font-variant: small-caps;"
-|Figure K
-|Figvre K
-|- style="font-family: times, serif; vertical-align:top;"
-|Finally taking the sword in hand, and standing erect at the Centre, with the arm and the same sword stretched out to the side in a single line, the point going down to touch the ground in an acute angle, as shown in figure K, we can see that the tip of the sword is just on the Circumference: in such a way that one could mark it on the pavement with just the single sword held in hand, without leaning. In any case, it is more expedient in something so important, to follow the order which we listed, above; more so as it is nearly impossible, just in turning around, to keep it steady and round as needed, to mark the circumference. Moreover, there is nothing more accurate than to put one of the ends of the cross-guard at the Centre point, and use the point to draw the Circumference, so the all rest can be drawn with confidence.
-|Finalement ſi on prend ceſt eſpee au poing, & qu’on ſe mette perpendiculairement debout ſur le Centre, avec le bras & la meſme eſpee eſtendus à coſté en droite ligne, la pointe tirāt vers la terre en angle aigu, comme il eſt repreſenté en ceſte figure K, on verra que la pointe de l’eſpee viendra juſtement ſur la Circonference: en ſorte qu’on pourroit deſcrir ſur le pavé avec la ſeule eſpee à tenir en la main, ſans aucun abaiſſement du corps. Toutesfois il ſera plus expedient en choſe de ſi grande conſequence de ſuivre l’ordre que nous avons baillé cy deſſus; d’autant qu’il eſt quaſi impoſſible, en tournant le corps pour deſcrire la dite circonference, de le gouverner & moderer ſi juſtement ſans varier, comme il ſeroit à ſouhaiter. Partant n’y a rien plus ſeur, que de le faire avec l’eſpee meſme, en mettant l’une des branches de la croix ſur le point du Centre, & tirer la Circonference avec la pointe, pour venir tant plus ſeurement à l’accompliſſement du reſte.
-|- style="font-family: times, serif; vertical-align:top;"
-|One could propose other considerations concerning the correct length of the sword: but is seems to me that enough has been said for those who like the elegance of wearing a sword by their side, the ease of drawing, the advantage of using it under all circumstances, and, principally, the necessity even, for those who would practice our training, using our Circle. Use will give them a good understanding of the need for this length and without this it would be impossible to understand the demonstrations of our precepts.
-|On pourroit propoſer encor d’autres conſiderations touchant ceſte juſte longueur de l’eſpee: mais il me ſemble que c’en eſt aſſez dit à ceux qui aiment la bien-ſeance de porter l’eſpee à coſté, la commodité de la tirer, l’avantage de la manier en toutes occurrences, & principalement la neceſſité meſme, pour le regard de ceux qui voudront prendre la peine de faire exercice à noſtre mode, & ſur le plan, de noſtre Cercle: car l’uſage leur en fera bien entendre la neceſſité, & que ſans icelle il leur ſeroit impoſſible de comprendre les demonſtrations de nos preceptes.
-|- style="font-family: times, serif; vertical-align:top;"
-|Because we have discussed the correct length of the sword, it would be reasonable if we finish by speaking, for the moment, as we did on the blade, about the entire hilt, or each of its parts. It is only reasonable that the observations which we have concerning arms, should be discussed before we come to the exercises. In any case we have found it best to put everything concerning the hilt in the next Plate, as this material cannot be deduced from this First Plate other than by bits as it appears in one image or another. It shall suffice for the present, to advise you to take a good look at the images of the hilt, which are at the bottom of the Plate and as seen from above in Circle No 1, until it can be discussed more fully with distinct description of all the parts in Plate II.
-|Puis que nous avons donc traitté de la vraye longueur de l’eſpee, il ſeroit raiſonnable que nous vinſſions à parler doreſenavant de la façon, tant au regard de la lame qu’au regard de la garde en ſon entier, ou en chaſcune de ſes parties; eſtāt raiſonnable, que les obſervations, que nous avons touchant les armes, ſoyent declarées avant que devenir à l’exercice meſme. Toutesfois nous avons trouvé bon de remettre ce qui touche la garde, au Tableau ſuivant, pour ce que la matiere n’en pourroit eſtre deduite en ce Tableau pemier, ſinon par loppins, comme il paroiſtra par les figures de l’autre. Il nous ſuffira donc pour le preſent, de vous advertir de prendre bon eſgard à la figure de ces gardes, qui ſont icy representées au bas du Tableau, & au plan du Cercle N.1. juſqu’à ce qu’il en ſoit diſcouru plus amplement avec diſtinćtion de caſcune des parties; ce qui ſera fait au Tableau II.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|CONCERNING the 12 SPANS
-of the blade and of Sliding the point of contact up and down the blade
-|TOVCHANT LES 12 NOMBRES
-de la lame, et de la gradvation et desgradvation
-|- style="font-family: times, serif; vertical-align:top;"
-|Speaking again of the blade and explaining the significance and use of the 12 Spans, by which the length is divided into 12 equal parts, as shown on the bottom of the Plate on both sides; the left side numbered, the right side of the same length, also numbered with twelve points, with each of the twelve Spans inscribed in Latin, corresponding the the twelve parts of the ancient Roman Pound weight.
-|Parlons derechef de la lame, & expliquons la ſignification, & l’uſage de ces 12. Nombres, par leſquels elle eſt diviſée en 12. parties egales de longueur, comme il ſe voit au bas du Tableau à la main gauche; le ſemblable eſtant auſſi repreſenté au coſté oppoſite, ſur une autre lame de la meſme longueur, diſtinguée pareillement par nombres en douze points, & par des noms, empruntez du Latin, en douze parties, reſpondantes au douze parties de la livre Romaine à l’ancienne.
-|- style="font-family: times, serif; vertical-align:top;font-variant:small-caps;"
-|All that is needed to follow all sorts of demonstrations are these 12 spans that divide the blade by degree of strength, from the tip to the crosspiece. These are of such importance that there will always be more to discuss no matter how much is already written. Because the principle advantages for practical work, for certainty in demonstrations, for understanding the relative weights, for governing  sensitivity of the hands, for attending to timing, and to approaches, are all found in whole or for the most part in the use of these Spans.
-|Il n’y a rien plus neceſſaire, pour examiner tout ſorte de demōſtrations, que ces 12. Nombres, par leſquels la lame eſt diſtinguée en autāt de degrez de force, en allant depuis la pointe juſqu’à la croiſee: & ſont de ſi grande importance, que jamais on n’en pourra tant eſcrire, qu’il n’en reſte encor à dire d’avantage. Pource que les principaux avantages de la Pratique, la certitude des demonſtrations, les proportions des poids, la moderation du ſentiment, les addreſſes des temps, & des approches, ſe trouvent toutes, ou en leur total, ou en leurs principales parties en l’uſage de ces Nombres.
-|- style="font-family: times, serif; vertical-align:top;"
-|The first point one mus know is that the twelve degrees of strength begin at the tip, the weakest part, and run up the blade, each section increasing strength by degrees up to the strongest part, the crosspiece of the hilt.
-|Touchant quoy il faut premierement ſçavoir, que ces douze degrez de force commencent depuis la pointe de la lame juſqu’à la croix de la garde: & que la pointe c’eſt le foible de l’eſpee; la garde c’en eſt le fort; ce qui eſt entre deux, tirant de la pointe vers la garde, ſe renforce tout de ſuite de degré en degré.
-|- style="font-family: times, serif; vertical-align:top;"
-|People wrongly attribute actions to the sword, but the sword itself is nothing more than a lifeless, immobile, material object, which only comes alive only through the hand that guides it. Yet because the liveliness of the sword depends only on the hand, it follows that the partition that is closest and most affected by the power of the hand should also be the strongest, those further away must consequently be weaker. The one that is first and most immediately affected by force from the hand, is called the strong part of the sword, point number 12. The partitions which receive power from the previous one and transmit it to the next and weaker one are said to be more or less strong or weak, according the the number of degrees along the blade. The last partition, preceeded by all the others, is called the weak part.
-|Car l’eſpee n’eſtant qu’une choſe materielle, eſt d’elle meſme ſans acune vigueur, & immobile, recevent toute ſa force de la main, qui la gouverne; de la quelle auſſi dependent toutes les aćtions, qui ſont attribuées improprement à l’eſpee. Et partant, puis que toute ſa vigueur depend de ceſt main ſeule, il faut neceſſairemēt, que la partie, qui en eſt plus proche & plus propre à recevoir ſon influence, ſoit auſſi la plus forte; celle qui s’en eſloinge, ſoit auſſi conſequément plus foible. Celle qui reçoit l’influence de force immediatement & la premiere de toutes, ſoit dite le fort de l’eſpee, cōme le point 12. Celles qui la recoivent mediatement par des autres precedentes, & la communiquent derechef à d’autres parties ſuivantes & inferieures, ſoyent dites plus ou moins fortes ou foibes, ſelon le nōbre des degrez qu’ils portent. Celle qui la reçoit la derniere de toutes, & par le moyen de toutes les autres precedentes, ſoit dite le foible.
-|- style="font-family: times, serif; vertical-align:top;"
-|Finally, the reason why I chose the number 12 and not another, was to keep the sword in proportion to the length of the arm, which is two cubits, while the sword is three, and as we showed above, that the blade being equal to the half-diameter and he arm equal to only one third, as the Diametre is divided into 24 partitions, the arm into 8, and so consequently the blade into 12.
-|Au reſte la cauſe pourquoy nous avons plustoſt choiſi ce nombre de 12. que nul autre, c’a eſté pour garder la proportion de ceſte longueur de la lame au bras de la perſonne: qui eſt de deux coudees, & l’eſpee de trois, auſſi a il eſté dit & demonſtré cy deſſus, que la lame eſt egale à la moitié du Diametre, & le bras n’en eſt egal, qu’à un tiers, de ſorte que le Diametre eſtant 24. le bras ſera 8. & la lame par conſequent 12.
-|- style="font-family: times, serif; vertical-align:top;"
-|Those who divide the blade into two equal parts, known as strong and weak, with the weak starting from the tip to the middle and the strong from the middle to the hilt, have made note of some difference between the partitions, but not enough.
-|Ceux qui l’ont partie en deux moitiez egales, aſſavoir au fort & au foible: commençant le foible depuis la pointe juſques au milieu, & le fort de là en avant juſques à la garde, y ont bien remarqué quelque difference de parties; mais inſuffiſament.
-|- style="font-family: times, serif; vertical-align:top;"
-|There are others who have divided the blade into three equal parts, with a middle section between the strong and the weak parts, because they have noticed that the middle section is sometimes used as a strong part, sometimes as a weak part.
-|Il y en a eu d’autres qui l’ont diſtinguée en trois parties egales, mettant entre le fort & le foible le mediocre: par ce qu’ils remarquoyent que le milieu de l’eſpee participe de l’un & de l’autre, & qu’on s’en ſert tantoſt comme dufort, & autresfois comme du foible.
-|- style="font-family: times, serif; vertical-align:top;"
-|Others, following the same logic, distinguish four parts: the strong, the semi-strong, the semi-weak, and the weak. But all without showing in their Style any evidence of use, or of noteworthy advantages or disadvantages of these differences.
-|D’autres ſuivants la meſme trace, ſont venus un peu plus avant, & l’ont diſtinguée en quatre parties, leſquelles ils ont nommées le fort, le demi-fort, demi-foible, & foible. Mais le tout ſans en monſtrer en toute leur Pratique aucun evident uſage, ou difference remarquable d’avantage, ou de deſavantage.
-|- style="font-family: times, serif; vertical-align:top;"
-|All these divisions of the blade into 2, 3, or 4 parts are insufficient, principally because when we consider two swords working at the same time, one against the other, it is impossible to distinguish with certainty which is the strong or the weak when divided into only 2, 3 or 4 parts. So suppose we distinguish the blades into 3 parts, and that we wish to press the medium against the weak part. It is impossible to do this with assurance: the measure of the weak goes from the tip to number 4, and the medium goes from 4 to 8, so that pitting the medium against the weak can mean the 7th Span against the first or the 4th against the 3rd. These two cases are so completely different in nature, that it is absolutely impossible to produce the same effects or demonstrate the same techniques. Thus it follows that if one does not divide the blade into enough parts, one cannot guarantee with certainty the same techniques, and therefore, we need to use a larger number. The most convenient is 12, which is proportional to the arm, as well as similar to the 12 parts of the Roman Pound, the Latin names of which are inscribed on the blade on the right hand bottom.
-|Toutes ces diviſions de 2. 3. ou 4. parties ſur la lame, ſont inſuffiſantes: & principalement  à cauſe qu’il faut icy conſiderer deux eſpees, qui travaillent à meſme temps enſemble, l’une contre l’autre: dont is ſeroit impoſſible d’en aſſigner aucune certaine diſtinćtion, du fort ne du foible, pour la grande meſure de chaſcune de ces 2. 3. ou 4. parties, en quoy la lame ſeroit diviſée. Car poſé que qu’elles fuſſent diſtinguées en trois parties, & qu’il fuſt queſtion de les accoupler, le mediocre avec le foible, je dis, qu’il ſeroit impoſſible de le pratiquer avec aſſurance: eſtant la meſure du foible, depuis la pointe juſques à 4. & du mediocre depuis le 4. juſques au N.8. en ſorte qu’on ne ſe pourroit reſoudre d’accouppler le Nombre 1. au N.7. de la lame contraire; ou le Nombre 3. avec le 4. car en l’un & en l’autre il ſe trouve le foible avec le mediocre. Etants toutesfois lesdits accouplements & aſſemblages des eſpees di ſi differente nature & condition, qu’il eſt abſolument impoſſible d’en tirer les meſmes effets, ne d’y faire paroiſtre les meſmes demonſtrations. Dont s’enſuit que quand on ne met aſſez de parties ſur la lame, qu’on en oſte auſſi par meſme voye toute la certitude des demonſtrations: & par tant, qu’il eſt neceſſaire d’en venir à un plus grand Nombre. Dont le plus convenable c’eſt celuy de 12. qui retient la proportion du bras avec l’eſpee, outre la ſimilitude des 12. parties de la livre Romaine, dont les noms Latins en ſont eſcrits au bas de ce Tableau ſur la lame, qui eſt à main droite.
-|- style="font-family: times, serif; vertical-align:top;"
-|The names are as follows: 1. Vecia, one ounce. 2. Sextans, the 6th part of a pound, or two ounces. 3. Quadrans, the quarter-pound. 4. Triens, the third, or four ounces. 5. Quincunx, five ounces. 6. Semis, the half-pound. 7. Spetunx, seven ounces. 8. Bes, two thirds, or eight ounces. 9. Dodrans, three-quarters, or nine ounces. 10. Dextans, ten ounces. 11. Deunx, eleven ounces. 12. As, the whole, either the pound or the sum. It was not only their custom to divide up pounds this way, but also from then to now entire inheritances, which is still done today amongst Jurists, to express through these names, the value of each of the parts.
-|Les noms en ſont tels qu’il s’enſuit. 1. Vecia, une once. 2. Sextans, la ſixieme partie de la livre, ce ſont deux onces. 3. Quadrans, le quart. 4. Triens, le tiers, qui ſont quatre onces. 5. Quincunx, cinq onces. 6. Semis, la demie livre. 7. Septunx, Sept onces. 8. Bes, deux tiers, ce ſont huit onces. 9. Dodrans, trois quarts, ce ſont neuf onces. 10. Dextans, dix onces. 11. Deunx, onze onces. 12. As, l’entier ſoit livre ou ſomme. Car ils n’avoyent pas ſeulement couſtume de diviſer ainſi les livres, mais auſſi à l’advenant d’icelles les ſommes entieres des heritages, ce qui ſe pratique encor aujourdhuy entre les Iuriſtes, pour exprimer par l’appropritation de ces dits noms, la valeur ce chaſcune des parties.
-|- style="font-family: times, serif; vertical-align:top;"
-|We could do the same, using these same or similar names for the 12 degrees of strength. But the best and most sensible way would be to simply use the use the numbers, by which the length of the blade is divided into 12 equal parts; which also reflects the relative strength of each, for, as explained above, as the parts by degree get closer to the hand, which controls the entire sword, they become stronger, and conversely, as they move away, become weaker. But be that as it may, it is of little import to us: for use does not require exact knowledge of the relative force, but we only to know which is greater and which is lesser, in order to act against the incoming blade, whether it is necessary to increase, to hold, or lessen the force, to overcome, or to cede to the counter-force.
-|Nous en pourrions auſſi faire le ſemblable, en nous ſervant de ces meſmes ou de ſemblables appellations, pour exprimer les 12. degrez de force. Mais le meilleur & le plus intelligible ſera de nous tenir ſimplement aux chifres, par leſquels ceſte lame eſt diſtinguée en 12. parties egales de longueur; n’empeſchant toutesfois rien, qu’elles ne ſoyent aucunement diſſemblables en puiſſance: car ainſi qu’il a eſté declaré cy deſſus, autant que les degrez s’approchent de la main, qui gouverne toute l’eſpee, d’autant ſeront elles trouvée plus fortes; & au contraire plus debiles. Mais quoy qu’il en ſoit, celà ne nous importe guere: d’autant que l’uſage ne requiert pas d’en ſçavoir ſi exaćtement la proportion, ains ſeulement de cognoiſtre le plus & le moins, pour ſe conduire à l’advenant, ſoit qu’il ſoit neceſſaire d’accroiſtre, ou de moderer, ou d’amoindrir ſa force, ou de ſurmonter, ou de ceder à la force contraire.
-|- style="font-family: times, serif; vertical-align:top;"
-|These are, in effect, the two goals, to which we aspire, and which can be found by means of these same numbers. The most important thing to know is precisely the amount of one’s own force, or of the opponent, as is necessary in practice, and next how to moderate, to increase, to diminish, this force as needed under different conditions, and as the occasion demands.
-|Et ce ſont en effećt lex deux intentions, qu’on devra pretendre, & les pourra on obtenir par le moyen de ces dits nombres. C’eſt aſſavoir premierement de congoiſtre preciſement la quantité de ſa propre force, ou de la contraire, tant qu’il eſt neceſſaire en la Pratique: & pour le ſecond de moderer, augmenter, & diminuer ſa dite force ſelon l’exigence de la diverſité, que les occaſions demandent.
-|- style="font-family: times, serif; vertical-align:top;"
-|The first point is very easy: because numbers that are equal in quantity are also equal in force. The difference in force is shown by inequality of the numbers. As 5 is 1 degree stronger than 4, & 6 is stronger by 2 degrees, and so on for the rest.
-|Le permier uſage en eſt fort facile: car les nombres egaux en quantité ſont auſſi egaux en force: la difference de force ſe demonſtrant par l’inegalité des nombres. Car 5 eſt 1 degré plus fort que 4, & 6 en eſt plus fort de 2. & ainſi du reſte à l’advenant.
-|- style="font-family: times, serif; vertical-align:top;"
-|The second point is easy to understand from the first one. Say my intent is to increase my force, I must assess and increase my own numbers. For example: if the blades are crossed 6 against 6, and I wish to increase my force, I change the point of contact so that the 7, 8, or 9 of my blade crosses with the 6 of the other sword; and by this means, I shall have increased my force 1, 2, or 3, or as many degress as I wish. If the intent is to diminish my force, the sword must be withdrawn towards the tip, so the point of contact moves to smaller numbers. This is what we call decreasing. Sometimes, one increases one’s own blade with the decrease of the opponent’s. For example, say two blades are in contact in the exact middle, which is in Span 6, and say that I move the point of contact so that mine becomes number 8, and my adversary to number 4; then that would mean an increase in my blade with a decrease on the opposing blade. Or, say, initial contact begins with unequal numbers, for example number 5 against number 8 and I change the point of contact by sliding the blades so that I bring my 8 or 9 against his 4 or 5: so that from three numbers weaker, I have moved to four numbers stronger. Contrarywise, one may decreases one’s own blade with an increase of the opposing blade, diminishing one’s own strength, and increasing that of the other party. Likewise, the increase of both swords happens at the same time, and likewise again, a double decrease.
-|Le ſecond point ſera facile à comprendre par le premier. Car s’il eſt queſtion d’augmenter ſa force, il faut graduer & augmenter ſes nombres. par example: si les lames ſont aſſemblées 6. contre 6. & que je veuille augmenter ma force, je les reculeray en telle ſorte, que le 7. 8. ou 9. de la mienne, ſe viennet accoupler avec le 6. de l’eſpee contraire; & par ce moyen j’auray augmenté ma force, de 1, 2, ou 3, ou autant de degrez, que je voudray. S’il eſt question de la diminuer, il la faudra reculer devers la pointe, qui en eſt le foible, en ſorte que l’aſſemblement en vienne à moins de nombres. C’eſt que nous appellons deſgraduer. Aucunefois on fera la graduation de ſa propre lame avec degraduation de la lame contraire: par example. Soyent accouplées les deux lames chaſcune au juſte milieu, qui eſt au Nombre 6. & que je tranſmue tellement le point de l’attouchement, que la mienne vienne au nombre 8. & celle de ma partie adverſe au nombre 4; alors ſera faite la graduation avec la degraduation de la partie contraire. Ou que l’accouplement ſoit premierement de nombres inegaux, par example, du nombre 5. contre le nombre 8. & qu’on change tellement le point d’attouchement par la raclure des eſpees, qu’on en mene le 8. ou 9. contre le 4. ou 5. de la partie adverſe: en ſorte que de trois nombres plus foible, on vienne à ſe rendre de quatre nombres plus fort. Il adviendra auſſi au contraire, qu’on fera la deſgraduation de ſa propre lame, avec graduation de la lame contraire, diminuant ſes propres forces, & augmentant celles de ſa partie. Aucunefois on en fera la graduation de toutes les deux eſpees enſemble: & aucunesfois derechef double degraduation.
-|- style="font-family: times, serif; vertical-align:top;"
-|The same things may be done with blades when they are not divided into 12 parts, but this will be ragged, and without any certainty of results; likewise when showing a proof, or wishing closer examination of some interesting aspect that comes about from a particular crossing of swords, it would be impossible to make any display of the contact, or to recreate a situation, which is, of course, absolutely necessary each and every time one wishes to examine any operation, without exception, whatever it may be.
-|Les meſmes effećts ſe pourroyent auſſi pratiquer avec des lames qui ne fuſſent pas diſtinguée en ces 12. nombres: mais ce ſeroit comme à taſtons, ſans aucune certitude: auſſi quand il ſeroit queſtion d’en faire les preuves, ou d’examiner quelque beau trait, qui ſe ſeroit preſenté à l’occaſion de l’accouplement des eſpees, il ſeroit impoſſible, de faire aucune demonſtration de l’attouchement, ou de la ſituation; ce qui eſt toutesfois neceſſaire toutes & quantesfois qu’il ſe preſente à examiner aucune operation, ſans nulle exception, qui puiſſe eſtre.
-|- style="font-family: times, serif; vertical-align:top;"
-|If one can imagine, that it is absolutely necessary to know exactly the proportions of all unequal forces, to make use of all their advantages, but that adroitness, which it gives us, is not enough to fully comprehend all the differences. If two blades are crossed, for example 2 against 4 or 10 against 8, the difference between the stronger and weaker numbers in each case is the equal to 2. But the relative values are not the same when we come to compare these two different cases to each other, they will be proportionally significantly different, because 4 is the double of 2, but 8 is only one third more than 6. In this way the relative proportions of force are unequal, even when the numeric differences are equal. Because the proportional difference between these numbers, when we compare two numbers to two other numbers, will always lessen as they approach the hilt, as the lesser of the two numbers becomes greater; so the proportion of the difference between 2 & 3 is found to be greater than the proportional difference between 3 & 4 or between 4 & 5 and so on, the differences becoming ever smaller, as the numbers become larger.   It might seem to some that we should simply make a list of the relative differences, by point of contact along the sword, and so one could quickly see and work with the proportional increase or decrease of forces, for each point of graduation along the blades.
-|Si quelqu’un s’imagine, qu’il ſoit abſoluement neceſſaire de cognoiſtre exaćtement les proportions de toutes les forces inegales, pour ſe ſervir à touts propos de leurs avantages; & que l’adreſſe, que nous en baillons, n’eſt pas ſuffiſante pour en comprendre à plein toutes les differences. Car ſi les deux lames ſont accouplées, par example 2. contre 4. ou 10. contre 8. la difference in ſera egalement de deux nombres plus fort ou plus foible, auſſi bien en l’un qu’en l’autre de ces deux accomplements: mais quand ce viendroit à comparer ces deux differences l’une à l’autre au regard des nombres, qui ſont diſſemblables, la proportion en ſeroit grandement differente: à cauſe que 4. eſt le double de 2. & 8. n’eſt qu’une troiſieme partie plus que 6. de maniere que les proportions de force ſont ſouventesfois inegales, nonobſtant que les nombres de leur difference ſoyent egaux. Car les proportions des differences des nombres, qui ſont mis en compariſon deux & deux contre deux & deux autres, vont touſiours en amoindriſſant à l’advenant, que le moindre de cesdites deux Nombres à comparer enſemble s’augmente; ſi que la proportion de la difference, qui eſt entre 2. & 3. eſt trouvée plus grande, que celle qui eſt entre 3. & 4. ou entre 4. & 5. & ainſi conſequemment; eſtant touſiours les differences plus petites, à meſure que les nombres s’aggrandiſſent. Dont il ſemblera par adventure à un tel, que nous devions expliquer l’inegalité de toutes ces differences par le menu, & aſſigner à chaſcun accouplement d’eſpees ſa proportion, afin qu’on peuſt ſçavoir par ce moyen, combien c’eſt qu’on augmente ou diminue la proportion de ſes forces, avec chaſcune ſorte de graduations, petites ou grandes, telles, qu’elles pourront eſtre, & ſur tels endroits des lames, où on les voudra mettre en oeuvre.
-|- style="font-family: times, serif; vertical-align:top;"
-|To the above, I would respond, that it is true, the proportional differences change, increasing or decreasing inversely with numerical values of the point of contact. Consequently, as the numbers, against which we measure the graduation, become larger, one must make larger increases towards the hilt to make any gains. And yet, as these numbers become larger, we have less ability to increase them. Nevertheless, it is enough to have a general awareness, without needing a close examination of the details. Technically, the force between the two swords can always be considered equal, since both swords have12 partitions. If two blades come together unequally, for example, one blade contacts at number 7 and the other at number 4, they will behave differently against each other, one with more, the other with less force; but alternatively, the sword at number 4 can reinforce itself with a graduation of 8 degrees up to 12, whereas the sword at number 7 can increase to 12 by only 5 degrees, because the number of partitions of the swords are equal. Because such a large change can happen in a moment, & this is even expected, it is enough to know the difference in forces from the number of degrees, which can easily determine if the difference is large, medium, or small. Because 1 degree is a little stronger, 2 degrees is evidently more, and 3 degrees is much more. Those are all the distinctions we need, since seeking to know exactly all the relative proprotions of each and every possible crossing of swords that can be imagined is not only impossible to observe at speed in our training, but it would also be useless.
-|Là deſſus je luy reſpondray, que c’eſt la verité, que les proportions des differences ſe changent, en augmentant & en diminuant au rebours de l’accroiſſement de leurs nombres: & par conſequent, d’autant que les nombres, contre leſquels on fera la graduation, ſeront plus grands, auſſi faudra il faire à l’advenant la dite graduation plus grande pour gaigner quelque choſe: & au rebours, d’autant que les nombres, avec leſquels la graduation ſera faite, ſeront plus grands, d’autant en pourra eſtre la graduation plus petite. Et cependant il ſuffit d’avoir de cecy une cognoiſſance generale, ſans qu’il ſoit beſoin d’en examiner les particularitiez. Car s’il faut parler proprement, la force des deux eſpees eſt touſiours egale. Car elles ſont toutes deux comme 12. S’il advient qu’elles ſoyent accouplées inegalement; par exemple, le nombre 7. de l’une au nombre 4. de l’autre, il eſt bien vray qu’elles ſont alors diverſement gouvernées, l’une avec plus, & l’autre avec moins de puiſſance; mais en eſchange il faut conſiderer, que l’eſpee de 4. ſe peut renforcer en un inſtant juſqu’à 12, augmentant ſa force par la graduation de 8. degrez entiers; là ou l’eſpee de 7 ne ſe peut renforcer, que juſqu’à 12. pareillement, qui ne font que 5 degrez, à cauſe que les nōbres des eſpees ſont egaux. Puis qu’il peut donc advenir un ſi grand changement en un moment de temps, & meſmes qu’on le doit comme pour certain attendre, qu’il nous ſuffiſe de ſçavoir la difference des forces par le nombre des degrez: leſquels nous peuvent aſſez declarer ſi la difference en eſt grande, petite, ou moyenne. Car 1. degré, c’eſt un peu plus fort: 2. degrez, c’eſt evidement plus: 3. degrez, c’eſt beaucoup plus. Voilà les diſtinćtions, qui nous doivent ſuffire. Car de vouloir ſçavoir exaćtement toutes les proportions de tant & tant aſſemblages d’eſpees, qu’on pourroit imaginer, ne ſeroit pas ſeulement impoſſibe à obſerver en des occaſions ſi viſtes, comme ſont celles de ceſtuy noſtre Exercie, mais il ſeroit auſſi inutile.
-|- style="font-family: times, serif; vertical-align:top;"
-|Finally, all we have said up to now about the gradation of the sword, must be understood simply with regard to these twelve numbers, by which one adjusts one’s own force and likewise counters the opposing force, notwithstanding that there are still other aspects to consider, each of which shall be discussed, in its proper place.
-|Au reſte tout ce qui eſt dit juſqu’à preſent touchant la graduation & deſgraduation des eſpees, pour moderer par icelles ſa propre force, & pareillement la force contraire; ſe doit entendre ſimplement au regard de ces douze nombres, ce qui n’empeſche toutesfois qu’il n’y ait encor pluſieurs autres manieres de renforcements: deſquels il ſera traité, de chaſcune en ſon propre lieu.
-|- style="font-family: times, serif; font-size: 16pt; vertical-align:top;font-variant: small-caps"
-|HOW TO HOLD
-the sword in the hand to practice the drills
-|LA MANIERE DE TENIR
-l’espee av poing, povr pratiqver nos receptes.
-|- style="font-family: times, serif; vertical-align:top;"
-|The last point illustrated on this Plate concerning the sword is the manner of holding it, which is quite different from other methods. As is shown, on the two numbered swords at the bottom, place the index finger over the exterior branch of the crosspiece, and wrap it around the end of the blade, and the thumb either over, or around, the crossguard likewise inside the guard, with the rest of the fingers wrapped around the handle, so it lies in the hollow of the palm, with the crosspiece held horizontally.
-|Le dernier point qui eſt repreſenté en ceſt Table touchant l’eſpee, c’eſt la maniere de la tenir au poing, grandement differente de l’ordinaire des autres. Car ainſi qu’il eſt exprimé icy bas en ces deux eſpees nombrées, nous mettons le doigt indice dans la garde par deſſus la branche exterieure, & alentour du talon de la lame, & le pouce à l’autre coſté, ſur la branche interieure, ou alencontre, par dedans la garde pareillement, avec le reſte des doigts bien eſtoitement ſerrez alentour de la poignee, en ſorte que le pommeau ſoit affermi dedans le creux du poignet, & les branches horizontales, l’une à coſté de l’autre.
-|- style="font-family: times, serif; vertical-align:top;"
-|It is absolutely necessary for all those who would learn anything of our Style, to hold the sword in this way, and not in any other; this grip is the only sure way to perform most of the operations, and is the foundation of the best sword-work for the thrust, either to aim, or to defend. This confidence is principally founded on the proper angle of the crosspiece, and on the force of the blade, held in this said manner. This shall be discussed further elsewhere, where the comparison of this grip to others, shall evince the superiority, through the coming together of the effects and  advantages of this grip compared to all others.
-|Il eſt abſoluement neceſſaire à touts ceux qui voudront faire aucune recerche de noſtre Pratique, de faire l’empoignement de l’eſpee en ceſte ſeule maniere, & non pas en quelque autre ſorte, que ce ſoit: d’autant que de ceſte ſeule depend la certitude d’une bonne partie de toutes les operations, & y ſont fondez les plus nobles exploits des eſtocades, à tirer, ou à defendre; dequoy l’aſſeurance eſt principalement fondeée ſur la ſituation de la croix, & ſur la force de la lame, tenue en ceſte maniere dernierement dite.  dont il ſera diſcouru autrepart; où nous mettrons en comparaiſon, & en ferons paroiſtre l’excellence, par la conference des effećts & des avantages de ceſte cy au regard de toutes les autres.
-|- style="font-family: times, serif; vertical-align:top;"
-|The practical point of this discussion on the concurrence of the Circle, the Sword, and the Human Body has been to show how easy it is for everyone to have a sword of the proper size.
-But there is a concern about the permanently-inscribed Circle, wherein one must oftentimes test between people of unequal stature, for which each should have his own properly-sized Circle, or between people of equal size, but who are both either larger or smaller than the Diameter, such that the Circle is not drawn proportionally to their bodies.
-To minimize this inconvenience, the permanent Circle should be drawn to the proportions of an average person, to accomodate everyone.
-Those who are larger can make the ranges of their Instances a bit larger.
-Such as the first, outside the Circumference, a bit inside the Quadrangle.
-The second, near the middle of the Inside Square, a bit outside, on the oblique Diameter.
-And the third, likewise, a bit outside the Circumference, on the extended Perpendicular Diameter.
-Those smaller can shorten all the distances of their Instances against the opponent; and take the first, in contrast to those larger, a bit inside the Circumference along the Diameter.
-The second on the Oblique Diameter, a bit inside.
-And the third, again on the Perpendicular Diameter inside the Circumference.
-That is how the Circle can be of use to all sorts of people, without ever changing it.
-Thus I am quite certain this explanation is sufficient proof of the usefulness of both these two lengths, of the Sword, which, as I say, is the instrument used for every action, and of the Circle, which is the terrain, containing the correct and proportional distances for the actions, so they may be exploited confidently.
-It is true, that we have been somewhat particular in the research of some parts of this treatise, such as the deduction of the range of the Instances, the graduations, of the proportions of the body, and several other similar things, which we have calculated exactly; nevertheless, those who have no knowledge of mathematics should not be discouraged.
-Because what we have done was more for the contentment of those who would make a close  study of our Theory, than it is something necessary for our Training.
-Other than that, we have tried to put everything in good order, so that each can easily distinguish between those things necessary for Practice, from those which are only for Theorists, as long as they read our writings attentively.
-|Pour venir à la Pratique de tout ce qui a eſté diſcouru, touchant la convenance du Cercle, & de l’Eſpee, avec le Corps de l’Homme; il eſt aiſé à un chaſcun d’avoir une Eſpee de ſa juſte meſure.
-Mais pour le Cercle, qu’on deſcrit une fois pour toutes, où il faut ſouventesfois faire des preuves avec perſonnes inegales de ſtature, aux quels il faudroit à chaſcun ſon propre Cercle; ou bien avec perſonnes egales, mais plus grandes, ou plus petites, que la ligne du Diametre, en ſorte que le Cercle ne ſeroit pas compaſſé à la proportion de leurs corps.
-Pour obvier à ces inconvenients, il le faut tirer ſur la meſure d’une perſonne moyenne, afin qu’il ſoit capable d’eſtre accommodé à toutes.
-Car les plus grands y pourront prendre les meſures de leurs Inſtances un peu largement.
-Comme, la permiere, dehors la Circonference un peu au dedans du Quadrangle.
-La ſeconde, pres le milieu du coſté du Quarré inſcrit, un peu au dehors, ſurle Diametre oblic.
-Et la troiſieme ſemblablement un peu au dehors de la Circonference, ſur le Diametre perpendiculaire prolongé.
-Les plus petits y raccourciront auſſi les meſures de leurs Inſtances à l’advenant; & en prendront la premiere au contraire des grands, un peu dedans la Circonference ſur le Diametre.
-La ſeconde ſur le Diametre oblic, un peu en dedans.
-Et la troiſieme derechef ſur le Diametre perpendiculaire au dedans de la Circonference.
-Voilà comment ce Cercle pourra ſervir à toutes ſortes de perſonnes, ſans qu’il le faille jamais changer.
-Or je m’aſſeure que ceſte explication ſera pour le commencement une preuve ſuffiſante de a grande utilité de l’une & de l’autre de ces deux meſures, de l’Eſpee di-je, qui eſt ‘inſtrumēt de toutes les operations, & du Cercle, qui eſt la deſcription du Terrain, contenant les vrayes & proportionnelles diſtances, correſpondantes aux operations, pour les exploiter avec aſſeurance.
-Il eſt vray, que nous avons eſté quelque peu curieux en la recerche de quelques parties de ce traitté, comme en la dedućtion de la meſure des Inſtances, des graduations, & de a proportion du corps, & en quelques autres choſes ſemblables, que nous avons calculées aſſex exaćtement: toutesfois il ne faut pas que ceux, qui n’ont point de cognoiſſance des Mathematiques, en perdent pourtant courage.
-Car ce que nous en avons fait, c’a eſté plustoſt pour le contentement de ceux qui voudront examiner de pres noſtre Theorie, que pour ce que la choſe fuſt d’elle meſme neceſſaire en l’Exercice.
-Outre ce que nous avons taſché de mettre le tout ſi bien par ordre, que chaſcun y pourra aiſement diſtinguer les choſes neceſſaires à la Pratique, d’avec celles qui ne ſont que pour les Theoriſtes, moyennant qu’il liſe noſtre eſcrit avec attention.
-|}
 {{master end}}
-===== Copyright and License Summary =====
+{{master begin
+ | title = Copyright and License Summary
+ | width = 100%
+}}
 For further information, including transcription and translation notes, see the [[Talk:{{PAGENAME}}|discussion page]].
-Images free for non-commercial re-use with attribution, courtesy of Reinier van Noort
+<section begin="sourcebox"/>{{sourcebox header}}
-http://www.bruchius.com/img/Thibault.zip
+{{sourcebox
+ | work        = Images
-Transcription by Bruce G. Hearns
+ | authors     = courtesy of Reinier van Noort
-Copyright is Public Domain Contribution
+ | source link = http://www.bruchius.com/img/Thibault.zip
-{{public domain contribution}}
+ | source title= Thibault.zip
+ | license     = noncommercial
-Translation by Bruce G. Hearns, all rights reserved. {{copyrighted}}
+}}
+{{sourcebox
+ | work        = Translation
+ | authors     = [[translator::Bruce G. Hearns]]
+ | source link =
+ | source title= Wiktenauer
+ | license     = noncommercial
+}}
+{{sourcebox
+ | work        = Transcription
+ | authors     = [[User:Bruce Hearns|Bruce G. Hearns]]
+ | source link =
+ | source title= Wiktenauer
+ | license     = noncommercial
+}}
+{{sourcebox footer}}<section end="sourcebox"/>
+{{master end}}
 == Additional Resources ==
 * Howden, Matthew. "[http://matthewhowden.wordpress.com/comparison-of-thibaults-circle-and-the-leiden-circle/ Comparison of Thibault’s Circle and the Leiden Circle]". ''Sworded Contemplations''. April, 2008. Retrieved 08 February 2015.
-* Majár, János and Zoltán Várhelyi. ''Thibault and Science I. Measure, Distances and Proportions in the Circle''. ''[[Acta Periodica Duellatorum]]'' '''2'''(1): 67-104. 2014. {{doi|10.1515/apd-2015-0014}}.
+{{bibliography}}
-* [[Gérard Thibault d'Anvers|Thibault, Gérard]]. ''Academy of the Sword''. Trans. John Michael Greer. Highland Park, TX: [[Chivalry Bookshelf]], 2006. ISBN 978-1891448409
 == References ==
-{{reflist|2}}
+{{reflist}}
 {{DEFAULTSORT:Thibault d'Anvers, Gérard}}
 __FORCETOC__
@@ Line 1,823: / Line 419: @@
 [[Category:Rapier]]
+[[category:old format]]